現在価値と割賦価値（２） | 午後はカフェで経済学

割引現在価値

前回の内容をふまえ、今回は「割引現在価値」を説明します。同じ100円でも、１年後にもらえる100円は、現在の100円とは同等に扱えません。換算レートを、以下のように $i$ と置きましょう。

「現在の $100$ 円 $=$ １年後の $100(1+i)$ 円」

両辺を $1+i$ で割れば、「現在の $\frac{100}{1+i}$ 円 $=$ １年後の100円」です。言い換えれば、１年後の100円の価値は、現在の $\frac{100}{1+i}$ 円だということです。この $\frac{100}{1+i}$ 円を、１年後の100円の「割引現在価値」と呼びます。

同様に、現在と10年後のお金を比べる時も、換算レート（１年当たり）を $i$ と置けば

「現在の $100$ 円 $=$ 10年後の $100(1+i)^{10}$ 円」

両辺を $(1+i)^{10}$ で割れば、「現在の $\frac{100}{(1+i)^{10}}$ 円 $=$ 10年後の100円」となります。 $\frac{100}{(1+i)^{10}}$ 円が、10年後の100円の割引現在価値です。

このように、未来のお金を現在の価値に直すことを「割引く (discount)」といいます。また、割引き計算に用いた $i$ は、「割引率 (discount rate)」といいます。割引率としては、「金利」がしばしば用いられます。

ここまで来れば足し合わせることができます。例えば「今日100円、１年後にまた100円もらえる証券」の割引現在価値は、次のようになります。

$\begin{eqnarray*}100 + \frac{100}{(1+i)}\end{eqnarray*}$

２年後にも100円もらえるならば

$\begin{eqnarray*}100 + \frac{100}{(1+i)} + \frac{100}{(1+i)^2}\end{eqnarray*}$

一般に、「今年も含め、 $n$ 年間毎年 $D$ 円もらえる証券」の割引現在価値は

$\begin{eqnarray*}D + \frac{D}{1+i} + \frac{D}{(1+i)^2} + \frac{D}{(1+i)^3} +\cdots + \frac{D}{(1+i)^{n-1}} \end{eqnarray*}$

また、「１年後から $n$ 年間、毎年 $D$ 円もらえる証券」であれば割引現在価値は

$\begin{eqnarray*}\frac{D}{1+i} + \frac{D}{(1+i)^2} + \frac{D}{(1+i)^3} +\cdots + \frac{D}{(1+i)^{n}} \end{eqnarray*}$

これらはすべて等比数列の和です。等比数列の和（２）の公式を用いれば、 $n$ が大きい場合でも素速く計算することができます。ためしに上の例を計算してみましょう。和の公式によれば

$\begin{eqnarray*}S &=& \frac{D}{1+i} + \frac{D}{(1+i)^2} + \frac{D}{(1+i)^3} +\cdots + \frac{D}{(1+i)^n} \\\\&=& \frac{1-\left(\frac{1}{1+i}\right)^n}{1-\left(\frac{1}{1+i}\right)}\cdot \frac{D}{1+i} \\\\&=& \left\{1-\left(\frac{1}{1+i}\right)^n \right\}\cdot \frac{D}{i}\end{eqnarray*}$

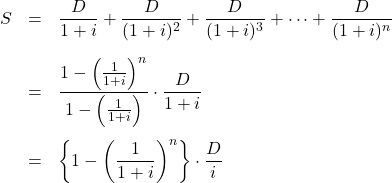
ですから、あとはここに $i$ ， $n$ ， $D$ の値を代入するだけです。

実際に使ってみましょう。金利が１％の世界では、１年後から20年後まで、毎年50万円払ってくれる証券の現在価値はいくらでしょうか。 $i=0.01$ ， $n=20$ ， $D=50$ 万円を代入すると、 $S=902.3$ 万円だと分かります。

さて、ここまでは将来の複数時点で支払われるお金を現在に割り引いて足し合わせることで、割引現在価値を求めるということを学びました。次回からはこれと逆の「割賦価値」について学びます。

>> 現在価値と割賦価値（３）割賦価値