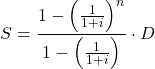>目次
第n項までの和(練習)
前回は以下の式を導出しました。
初項 ![]() ,公比
,公比 ![]() の等比数列の第
の等比数列の第 ![]() 項までの和は
項までの和は
![]()
今日はこの公式を練習してみましょう。経済学やファイナンスでよく出てくる足し算に、以下のようなものがあります。
![]()
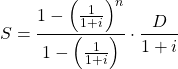
となります。もう少しきれいに整理できますが、それはみなさんにお任せしましょう。
類題です。
![]()
これも等比数列の和です。こちらは初項は
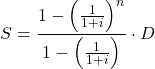
割引率
次回は
>> 等比数列の和(3)無限和の例
>目次
前回は以下の式を導出しました。
初項 ![]() ,公比
,公比 ![]() の等比数列の第
の等比数列の第 ![]() 項までの和は
項までの和は
![]()
今日はこの公式を練習してみましょう。経済学やファイナンスでよく出てくる足し算に、以下のようなものがあります。
![]()
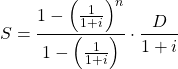
![]()