>目次

>> １，２，３，４，５

無限和の例


前回までは、初項 a，公比 q の等比数列を第 n 項まで足し合わせました。今回は無限に続く等比数列の全ての項を足し合わせることを考えます。すなわち

    \begin{eqnarray*}a + aq + aq^2 + aq^3 + \cdots \end{eqnarray*}


です。q が１以上だと、この和は無限大になってしまうのですが、-1 < q < 1 であれば、有限の値になります。公式の導出は次回にまわして、今回は例を２つ紹介しましょう。


例えば 面積が1/2平方メートルの土地、1/4平方メートルの土地、1/8平方メートルの土地・・・を全て足し合わせた広さはどれくらいでしょうか。式で表すと、

    \begin{eqnarray*}\frac12 + \frac14 + \frac18 + \frac{1}{16} + \cdots\end{eqnarray*}


これは初項1/2，公比1/2の等比数列の無限和です。無限個のものを足し合わせるのですが、答えは無限大にはなりません。それを表現したのが以下の図です。




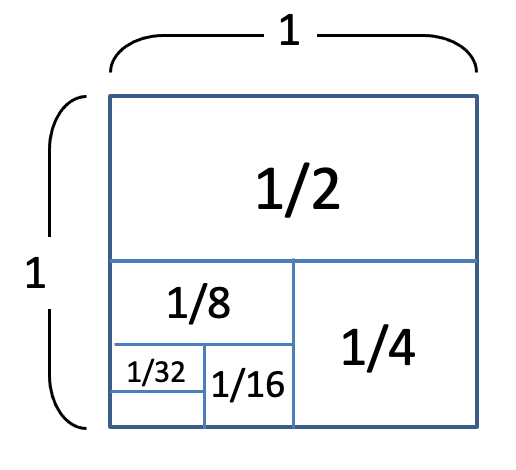
広さ1/2のタイル、1/4のタイル・・・と敷き詰めていくと、結局は縦横１メートルの正方形の領域に収まることが分かります。


もう一つ例を紹介しましょう。それは

    \begin{eqnarray*}0.99999999999999\cdots\end{eqnarray*}


と、どこまでも永久に9が続く少数です。私が小学生のとき、塾の先生が「これは１に等しい」と言い、クラスみんなで猛反発したのを覚えています。どこまで9が続いても、絶対に１にたどり着かないのだから、１に等しいわけはない、というのがその理屈です。でもこれは１に等しいのです（注1）。


「0.9999\cdots=1」は、次回勉強する等比数列の無限和の公式を使って証明することができます。というのも 0.99999\cdots を分解すると


    \begin{eqnarray*}0.99999999\cdots = 0.9 + 0.09 + 0.009 + \cdots\end{eqnarray*}



となり、初項0.9，公比0.1の等比数列の無限和とみなすことができるからです。


そこで、次回は等比数列の無限和を求めてみましょう。

>> 等比数列の和（４）無限和を求める

注1）
これは背理法でも証明できます。もし「0.9999\cdots \neq 1」ならば、必ずその中間の数字（小数）があるはずですが、0.99999\cdotsと1との間に別の数字を見つけることはできません。