割賦価値
複数年にわたって受け取るお金の合計価値を求めるのが「割引現在価値」の計算です。今日のテーマはこれとは逆の「割賦価値 (annuity value)」の計算です。
例えば退職金や宝くじの当選金などを想像してください。今すぐ一括で1000万円受け取ってもいいが、「◯年間、毎年同額ずつ受け取れる」という選択肢もあったとします。例えば1000万円を来年から毎年 ![]() 円、20年間に渡って受け取れるといった具合です。このとき、
円、20年間に渡って受け取れるといった具合です。このとき、![]() 円はいくらが妥当でしょうか。
円はいくらが妥当でしょうか。
「1000万円を20年で割るんだから50万円でしょ?」と言う人は損することになります。20年後の50万円の現在価値は、50万円よりも安いからです。前回出てきた式をもう一度見てみましょう。
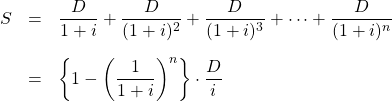
「20年間に渡って毎年
これを求めるためには、公式を逆に使います。金利は1%だとして、
これは借金の支払いでも同じです。今日一括で返せば1000万円で済む返済を、年1回の20回払いにするとしたら、1回あたり
ここまで、将来n回の支払いが起こるような証券を考えてきました。次回からは、「永久的に」支払いが起こる場合を考えます。
>> 現在価値と割賦価値(4)コンソル債の割引現在価値
