生産のモデル化（５） | 午後はカフェで経済学

「労働節約型」の技術

前回はコブ・ダグラス型の生産関数を１つ紹介しました。

$\begin{eqnarray*}Y = AK^{\alpha} N^{1-\alpha}\end{eqnarray*}$

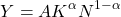
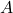
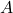
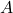
$A$ が２倍になれば、資本や労働の量が同じでも、２倍の産出が生み出せることが分かります。ですから $A$ は「技術水準」や「生産効率性」などを表すパラメータとみなされます。この $A$ には、「全要素生産性 (Total Factor Productivity)」という名前がついています。全ての要素、すなわち資本の生産性も労働の生産性も、同じように高めてくれるというニュアンスです。

今日はもう１つのコブ・ダグラス型の生産関数を紹介します。

$\begin{eqnarray*}Y = K^{\alpha} (AN)^{1-\alpha}\end{eqnarray*}$

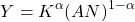
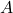
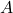
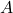
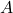
生産性を表す $A$ が、労働の投入量 $N$ の前についています。このような $A$ は「労働節約技術 (labor-saving technology)」を表したパラメータと言われます。 $A$ が倍の大きさなら、労働力 $N$ が半分でも済むからです。「労働節約」などと言うと、なんだか人の仕事を奪う技術のように聞こえますが、名前に惑わされてはいけません。「 $A$ が大きければ、同じ $N$ で今までよりたくさん生産できる」と言い換えることもできるからです。（例えばアメリカのフォードは、ベルトコンベアによる流れ作業を導入し、車を従来よりも少ない人数で生産できるようにしました。では従業員を解雇したかというとそうではなく、今までより多くの車を生産したのです。）

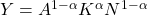
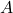
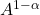
上記の２つの生産関数には、数学的な違いはほとんどありません。後者の生産関数を変形すると $Y = A^{1-\alpha} K^{\alpha} N^{1-\alpha}$ ですから、生産性を表す部分が $A$ か $A^{1-\alpha}$ かの違いはあります。しかし「生産性」はもともと抽象的なものですから、どちらで表しても良いのです。

どちらでも良いのですが、計算結果がきれいになるという理由で、有名な「ソローの経済成長モデル」では後者を使います。あとで出てきますので、今日紹介した２つめのコブ・ダグラス型も頭の片隅に置いておいてください。

これで生産関数の基本的な知識は習得できました。それでは、「経済成長論」の勉強に進むことにしましょう。

>> 経済成長論（序）