<< 序，１，２，３，４，５

収穫一定


前回は、労働や資本をインプットとする３つのタイプの生産関数を紹介しました。どのタイプでも、「投入量」を増やすと「産出量」も増えました。今日説明するのは、その「増え方」についてです。


たとえば料理をするとき、「１人分作るのも、２人分作るのもあまり変わらない」と言ったりします。１人分なら玉ねぎ半分のところが、２人分だと丸ごと１個切ることになったりはしますが、２倍の手間はかかりません。本当に２倍の手間をかけるとすれば、２人分よりも多い量が作れるでしょう。経済学では、原材料や手間などの投入量を m 倍したときに、作られる量が m 倍よりもっと多くなる状況を「収穫逓増（ていぞう）」（Increasing returns）と言います。生産すればするほど、効率が良くなっていくイメージです。グラフにすると以下のような感じです。横軸は投入量（労働）です。




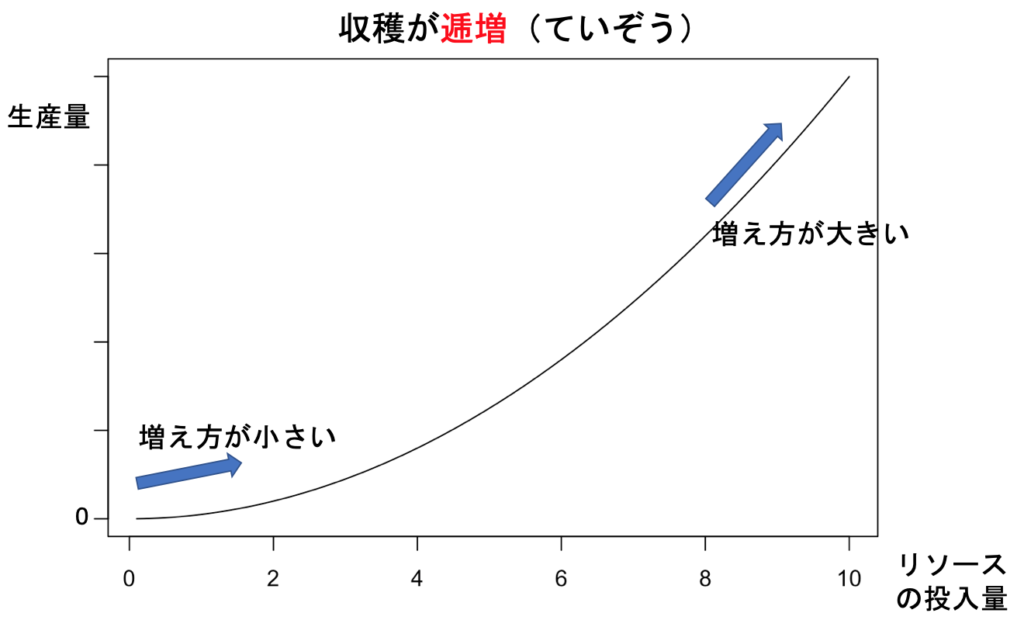
一方、勉強や仕事を既に5時間やって疲れて果てているとき、さらにもう5時間残業したとしても、達成される量は倍になりません。「投入量を m 倍したけど、産出は m 倍にはならない」という状況です。この状況を「収穫逓減（ていげん）」（Diminishing returns）と言います。投入を増やすにしたがって、生産効率が悪くなっていくイメージです。グラフにすると以下のような状況です。




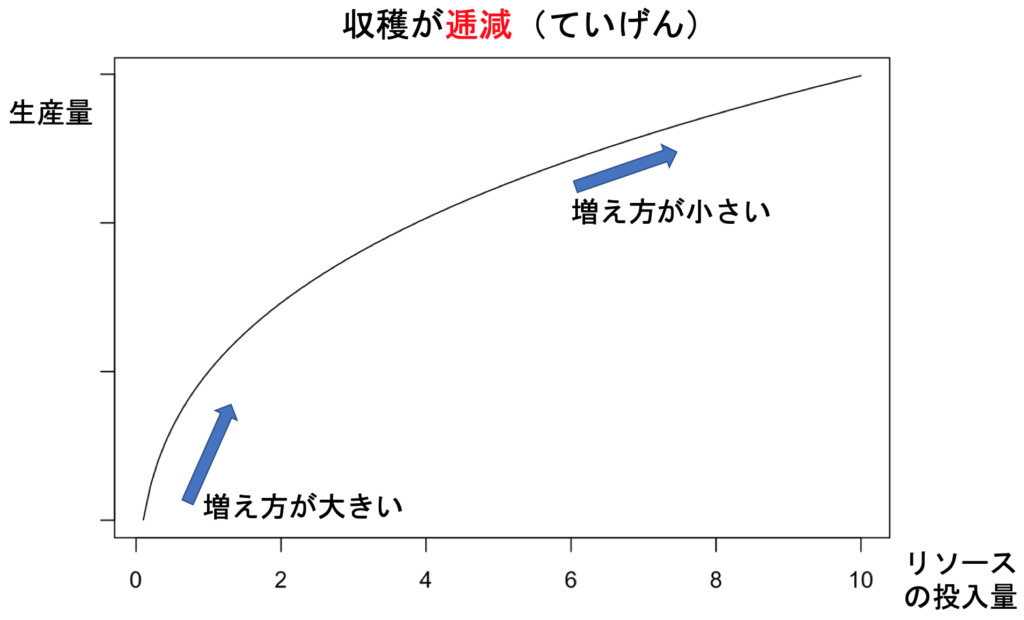
収穫の逓増と逓減は、大事な経済学用語です。私たちの日常でよくあるのは、「最初のうちは収穫逓増、そのうち収穫逓減」でしょうか。料理でも、勉強でも、投入量を増やしていくと最初のうちは効率が良くなっていくものですが、そのうちだんだん無駄が増えて非効率になっていきます。グラフにするとこんな感じです。




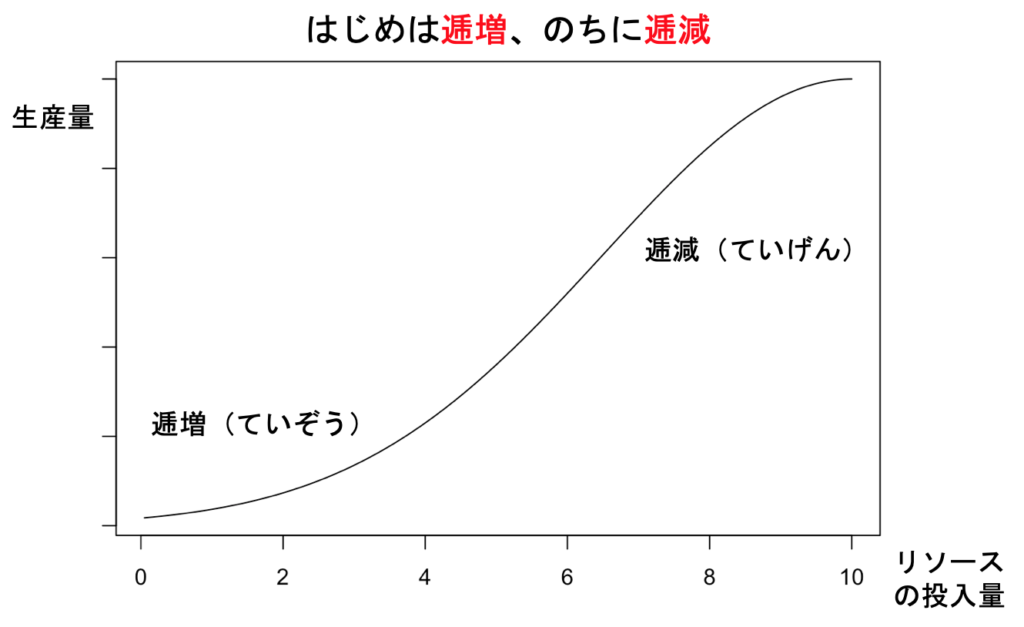
しかし、生産関数としては「最初は収穫逓増・のちに逓減」という複雑なものは普通は考えません。よく用いるのは「収穫一定」の生産関数です。収穫一定とは、「投入量を２倍、３倍、m 倍すると、産出も２倍、３倍、m 倍になる」という意味です。これは定義なので覚えてください。１変数関数であれば、これは「比例」とも呼ばれます。


収穫一定の定義は、投入するものが２つあっても同じです。例えば、前回出てきたコブ・ダグラス型の生産関数を考えてみましょう。K が資本、N が労働の投入量です。

    \begin{eqnarray*}Y = F(K, N) = AK^{\alpha} N^{1-\alpha}\end{eqnarray*}


ためしに、このコブ・ダグラス型の生産関数で、資本の量も労働の量も m 倍してみましょう。すると産出量もちょうど m 倍になることが証明できます。実際に K と N のところに mK と mN を代入すると、

    \begin{eqnarray*}F(mK, mN) &=& A(mK)^{\alpha} (mN)^{1-\alpha}\\&=&Am^{\alpha}K^{\alpha}m^{1-\alpha}N^{1-\alpha}\\&=&m^{\alpha}m^{1-\alpha} AK^{\alpha}N^{1-\alpha}\\&=& m AK^{\alpha}N^{1-\alpha}\\&=& mY\end{eqnarray*}


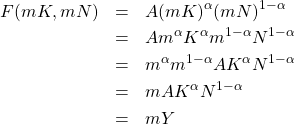
となり、確かに産出も m 倍になります。あくまで、資本と労働の両方を m 倍した場合です。労働を変えずに資本だけを m 倍したところで、収穫は m 倍にならないので注意してください。


最終回は、上記の生産関数を少しだけ変えた別バージョンのコブ・ダグラス型生産関数を紹介します。

>> 生産のモデル化（５）労働節約型の技術