マルサス・モデル３ シミュレーション編
前回学んだマルサス・モデルを、今回はシミュレートしてみましょう。初期時点（
）の人口は 
（１億人）とします。（これを基準化といいます。）土地の量は 
（５億ヘクタール）としましょう。
コブ・ダグラス型の生産関数 
の２つのパラメータは、
，
とします。また、人口増加率を決める関数 
として、今日は 
を使うことにします。これでひとまずシミュレーションを行い（シナリオ１）、そのあとで 
と 
の値を変えた別のシナリオでもシミュレーションをします（シナリオ２・３）。
・シナリオ１：
・シナリオ２：
・シナリオ３：
以下のグラフは、シナリオ１の結果です。時点 (
) が進むにつれて、人口 (
)，産出 (
)，一人当たりの消費 (
) がどう変わっていくかを表しています。
初期時点では土地が一人当たり５ヘクタールもあるので、一人当たりの消費も多めです。そこから人口が増加し（青い線）、それとともに生産も急増しています（赤い線）。増加のスピードは徐々に鈍っていきますが、
期目には人口は５億人、産出も５億トンほどになっています。
生活水準をあらわす一人当たりの消費はどうでしょうか。こちらは徐々に減少しています（緑の線）。最初の年では一人当たり1.7トンくらい消費していますが、最後は１トンまで下がっていることがわかります。生産よりも人口の増え方が速いためです。生活水準は落ち、最終的には人口の増加も止まっています。
シナリオ２では、土地の量を表すパラメータを 
に変えます。耕地が倍増したら、生活水準は上がるでしょうか。次のグラフが結果を表しています。縦軸のスケールがさっきとは異なることに注意してください。
土地がたくさんあるため、最初のうちは一人当たりの消費が多く、その豊かさゆえに人口は急増します。人口は最終的に10億人にまで増えています。一方、最初2.5トンあった一人当たりの消費は、最終的に１トンに落ち着いています。
最後はシナリオ３です。土地は最初と同じ 億ヘクタールに戻して、生産効率性を表す の大きさを２倍にします。収穫量の多い品種が発見されたイメージです。
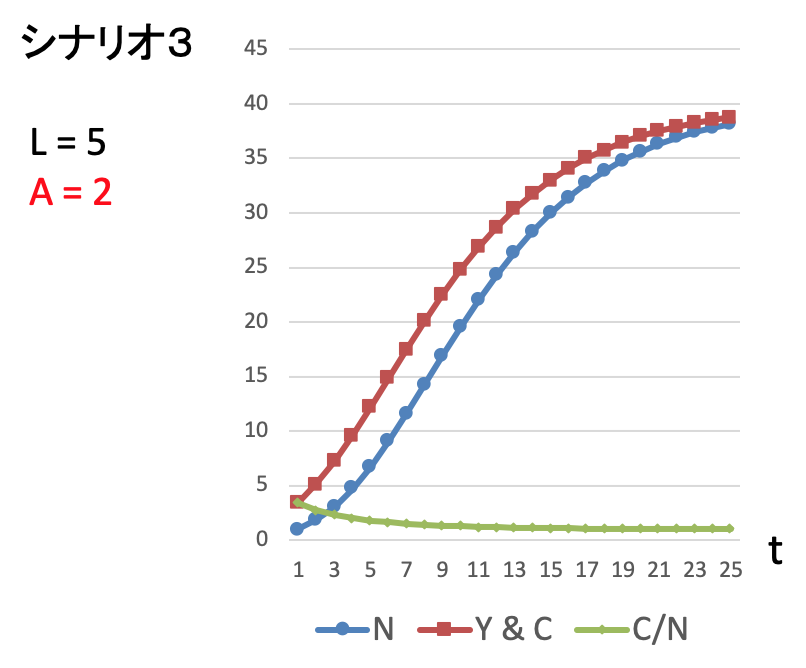
この場合、人口1億人でスタートした当初は、一人当たりの消費は3.5トンほどです。生活が豊かなので人口は急増し、最終的に40億人くらいで落ち着いています。その頃までには一人当たりの消費は結局1トンに落ち着きます。
どのシナリオでも、一人当たりの消費は最終的に1トンになっていることに気がつきましたか。これが「マルサスの罠 (Malthusian trap)」と呼ばれる筋書きです。土地が増えても、生産効率が上がっても、マルサス・モデルにとっては関係ありません。生活は一時的に豊かになりますが、人口がどんどん増加し、一人当たりの食いぶちが減るので、最終的な生活水準は土地の量や生産性が上がる前と変わらないのです。これがマルサス・モデルのシミュレーション結果です。
マルサスが危惧したことは、現代には当てはまりません。先進国で少子化が起こったり、貧しい国ほど人口増加率が高かったりする現状に、「豊かなほど人口が増える」というマルサスの仮定がそぐわないからです。マルサス・モデルは勉強にはなりますが、現状の分析には使えません。
さて、以前ピケティの数字で紹介したように、人類史が始まってから西暦1800年頃まで、人々の生活はほとんど豊かになりませんでした。人々の生活が豊かになり始めたのは、産業革命が進み、資本が蓄積されるようになってからです。経済成長理論にとって、資本の蓄積は不可欠なのです。そこで次回は資本の蓄積についてお話しします。
>> 経済成長論（４）資本の蓄積
