マルサス・モデル2 数式編
前回は、マルサス・モデルの概要を言葉で説明しました。今回は数式を使って説明します。
マルサス・モデルは過去から未来へと時間が流れていく「動学モデル (Dynamic model) 」です。最初の時点が ![]() で、
で、![]() ,3,4,
,3,4,![]() と時点が推移して行きます。(
と時点が推移して行きます。(![]() は time の頭文字です。)
は time の頭文字です。)
モデルの世界に存在する土地 (Land) の量は ![]() で表します。土地の量は次の期も、その次の期も変わらず一定です。また、この世界に存在する労働力、すなわち人口は
で表します。土地の量は次の期も、その次の期も変わらず一定です。また、この世界に存在する労働力、すなわち人口は ![]() で表します。(本来は働けない人もいますが、話を簡単にするため、人口と労働人口は同一視します。)土地と違い、人口は時間とともに変化するので、時点
で表します。(本来は働けない人もいますが、話を簡単にするため、人口と労働人口は同一視します。)土地と違い、人口は時間とともに変化するので、時点 ![]() の人口を
の人口を ![]() と表します。
と表します。![]() は
は ![]() での人口、
での人口、![]() は
は ![]() での人口といった具合です。初期の人口
での人口といった具合です。初期の人口 ![]() は所与(=あらかじめ与えられている値)です。
は所与(=あらかじめ与えられている値)です。

![]() 時点の産出の量を
時点の産出の量を ![]() で表します。
で表します。![]() はコブ・ダグラス型の生産関数(「生産のモデル化3」を参照)で決まると仮定します。農作物・家畜・木材などの生産量が、土地の量
はコブ・ダグラス型の生産関数(「生産のモデル化3」を参照)で決まると仮定します。農作物・家畜・木材などの生産量が、土地の量 ![]() と労働の量
と労働の量 ![]() で決まる様を想像してください。すなわち
で決まる様を想像してください。すなわち
![]()
土地の量は毎年増えないので、
資本主義においては、生産された物の一部が「投資」にまわされるのですが、マルサス・モデルでは投資は考えず、生産された物は全て消費されると仮定します。すなわち、総消費を大文字の
マルサスのモデルの重要な仮定は、「生活水準

人口増加率を決めるこの関数を ![]() で表します。
で表します。
ここまで出てきた連立「漸化式」をまとめると
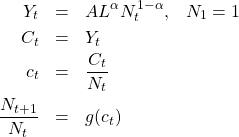
このモデルの外生パラメータは
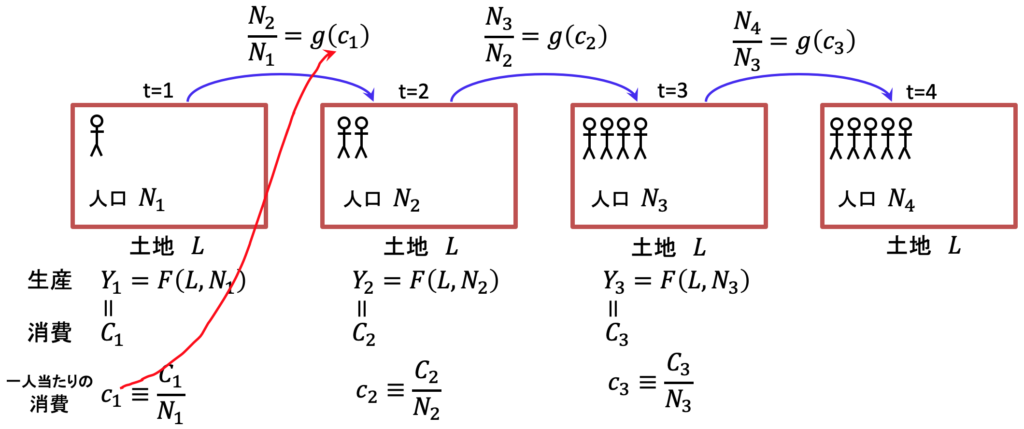
漸化式のことを大学では「差分方程式 (difference equation)」というので、私たちもそう呼ぶことにしましょう。次回はこれらの差分方程式をもとに、人口、産出、一人当たりの消費がどのように推移していくかシミュレーションしてみましょう。
>> 経済成長論(3)マルサス・モデル3 シミュレーション編
