等比数列の和（５） | 午後はカフェで経済学

経済学でよく登場する等比数列の無限和を求めてみましょう。経済学的な解釈は知らなくて構いません。初項と公比が何であるかを見極め、前回学んだ公式に当てはめてください。

問１（解答）

$\begin{eqnarray*}S=\frac{D}{1+i} + \frac{D}{(1+i)^2} + \frac{D}{(1+i)^3} +\cdots \end{eqnarray*}$

問２（解答）

$\begin{eqnarray*}S=D + \frac{D}{1+i} + \frac{D}{(1+i)^2} + \frac{D}{(1+i)^3} +\cdots \end{eqnarray*}$

問３（解答）

$\begin{eqnarray*}S=\frac{D(1+g)}{1+i} + \frac{D(1+g)^2}{(1+i)^2} + \frac{D(1+g)^3}{(1+i)^3} +\cdots \end{eqnarray*}$

問４（解答）

$\begin{eqnarray*}S=D + \frac{D(1+g)}{1+i} + \frac{D(1+g)^2}{(1+i)^2} + \frac{D(1+g)^3}{(1+i)^3} +\cdots \end{eqnarray*}$

問５（解答）

$\begin{eqnarray*}S=\frac{D}{1+i} + \frac{D(1+g)}{(1+i)^2} + \frac{D(1+g)^2}{(1+i)^3}+ \frac{D(1+g)^3}{(1+i)^4} +\cdots \end{eqnarray*}$

どうでしたか。このシリーズはひとまず終了です。ごくろうさまでした。

問１解答（問に戻る）

初項 $\frac{D}{1+i}$ ，公比 $\frac{1}{1+i}$ です。よって無限和は

$\begin{eqnarray*}S&=&\frac{\frac{D}{1+i} }{1-\left(\frac{1}{1+i}\right)} \\&=& \frac{D}{i}\end{eqnarray*}$

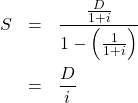
２行目の変形では、分子と分母の両方に $1+i$ をかけています。

問２解答（問に戻る）

初項 $D$ ，公比 $\frac{1}{1+i}$ です。よって無限和は

$\begin{eqnarray*}S=\frac{D}{1-\left(\frac{1}{1+i}\right)}\end{eqnarray*}$

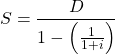
となります。もう少しきれいに整理できますが、それはみなさんにお任せしましょう。

問３解答（問に戻る）

初項 $\frac{D(1+g)}{1+i}$ ，公比 $\frac{1+g}{1+i}$ です。よって無限和は

$\begin{eqnarray*}S &=& \frac{\frac{D(1+g)}{1+i} }{1-\left(\frac{1+g}{1+i}\right)} \\&=& \frac{D(1+g)}{i-g}\end{eqnarray*}$

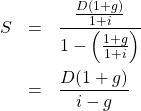
２行目の変形は、分母・分子の双方に $1+i$ をかけています。

問４解答（問に戻る）

初項 $D$ ，公比 $\frac{1+g}{1+i}$ です。よって無限和は

$\begin{eqnarray*}S&=&\frac{D}{1-\left(\frac{1+g}{1+i}\right)}\\ &=& \frac{D(1+i)}{i-g}\end{eqnarray*}$

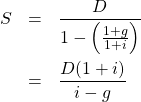
２行目の変形は、分母・分子の双方に $1+i$ をかけています。

問５解答（問に戻る）

初項 $\frac{D}{1+i}$ ，公比 $\frac{1+g}{1+i}$ です。よって無限和は

$\begin{eqnarray*}S&=&\frac{\frac{D}{1+i} }{1-\left(\frac{1+g}{1+i}\right)} \\&=& \frac{D}{i-g}\end{eqnarray*}$

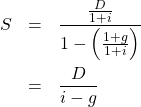
２行目の変形は、分母・分子の双方に $1+i$ をかけています。