>目次
無限和を求める
初項 ![]() , 公比
, 公比 ![]() の無限に続く等比数列の和を
の無限に続く等比数列の和を ![]() とおくことにします。すなわち
とおくことにします。すなわち
![]()
特に、初項が1の場合は
![]()
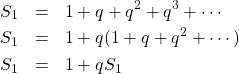
このように、第2項以下を
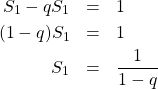
結果を公式として表しておきましょう。
等比数列の無限和の公式![]() のとき
のとき
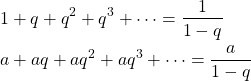
前回出てきた2つの例に当てはめてみましょう。1つめの例では ![]() ,
, ![]() ,2つめの例では
,2つめの例では ![]() ,
,![]() でした。公式を使えば
でした。公式を使えば
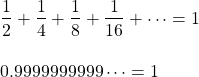
と分かります。やってみてください。
どうでしたか。等比数列の無限和の公式は、ぜひ導出のトリックも覚えてくださいね。次回の演習問題では、経済学でよく登場する等比数列の無限和を求めてみましょう。
>> 等比数列の和(5)無限和を求める(練習)
