目次へ

>> １，２，３，４，５，６，７，８

配当割引モデル


以前、「将来受け取れる配当の額が、株価にとっては大事だ」という話をしました。今日は一歩進んで、「将来受け取る配当の額から、株価がどう決まるか」を勉強しましょう。それを式で表したものが「配当割引モデル (Dividend Discount Model)」です。


配当割引モデルでは、将来受け取る配当の額は予想できるものとみなします。そこで、今日を時点0とし、１年後、２年後、３年後・・・に受け取る配当の期待値を、D_1, D_2, D_3, \cdotsとおきましょう。（D は“Dividend” の頭文字です。）


基本的には、株式の価値は、将来受け取る配当全てを合算した価値です。でも、D_1 + D_2 + D_3 + \cdots というように単純に足すことはできません。その理由は２つです。


１つめの理由は、「時間」です。１年後にもらえる1万円に比べたら、５年後にもらえる1万円の方が、待ち時間が長い分だけ価値は低いのです。ですから５年後にもらえる1万円はある程度「割り引いて」からでないと、１年後の1万円と一緒には扱えません。


２つめの理由は「リスク」です。将来の配当はあくまで期待値であって、実際にはそれより大きいことも小さいこともあり得ます。そして投資家は、同じ期待値ならリスクは小さいほどいいと考えます。１年後よりも３年後、３年後よりも５年後の未来の方が、経済や企業を取り巻く環境が不確かなので、（たとえ待ち時間を気にしない投資家であったとしても）５年後に期待される1万円は、１年後に期待される1万円と一緒には扱えません。


以上の理由から、「配当割引モデル」では、将来受け取る配当の期待値を、「割引率」を使って割引いてから足し合わせます。すなわち、割引率を k とすると、時点0の理論株価 P_0 は次のように表されると考えます。

    \begin{eqnarray*}P_0 = \frac{D_1}{1+k} + \frac{D_2}{(1+k)^2} + \frac{D_3}{(1+k)^3} + \cdots \end{eqnarray*}


たとえば割引率が7％であれば、k=0.07 です。k は、「配当が支払われるまでの待ち時間」と「将来の不確実性」の両方を反映しているため、「k= 金利＋リスク・プレミアム」と解釈されます。リスク・プレミアムは、投資家たちがリスクに対して要求する見返りです。金利は全ての株に共通しますが、リスク・プレミアムは株の銘柄ごとに異なる部分です。投資家たちが何らかのリスクを警戒する銘柄ほど、k の値は大きくなります。


ここで、配当が一定率 g で増加していくと予想されている成長企業の場合を考えてみましょう。つい最近支払われた直近の配当を D_0 とすると、１年後の配当は D_0(1+g)，２年後の配当は D_0 (1+g)^2 というように、毎年 (1+g) 倍で増えていくと予測される企業です。（g は「配当成長率」と呼ばれ、g<k だと仮定します。）このとき、配当割引モデルによる理論株価は

    \begin{eqnarray*}P_0 &=& \frac{D_0(1+g)}{1+k} + \frac{D_0(1+g)^2}{(1+k)^2} + \frac{D_0(1+g)^3}{(1+k)^3} + \cdots \\\\&=& \frac{(1+g)D_0}{k-g}\end{eqnarray*}


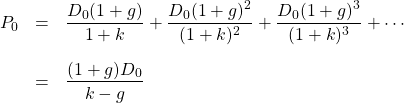
です。（２つめのイコールには「等比数列の無限和」が使われています。）株価は、現在の配当、配当成長率、割引率の３つで決まることが分かります。これが配当割引モデルです。


この配当割引モデルを応用して、株式投資の基本用語である「バリュー株」と「グロース株」についての理解を深めたいと思います。その準備として、次回はバリュー株とグロース株とは何かを説明します。

>> 配当割引モデル（６）バリュー株・グロース株１