株式の割引現在価値
ここまで、割引現在価値を求める例では、毎年もらえる金額は ![]() 円で一定という仮定でした。今回は、毎年もらえる額が「一定率で増えていく」場合の割引現在価値を考えてみましょう。
円で一定という仮定でした。今回は、毎年もらえる額が「一定率で増えていく」場合の割引現在価値を考えてみましょう。
例として、株式を考えてみましょう。株式の配当額は毎年一定ではなく、企業が成長していくにしたがって、年々少しずつ増えていくのが一般的です。いま、単純なケースとして、ある株の配当が「一定率 ![]() で成長していく」と予想されているとしましょう。すなわち1年後は
で成長していく」と予想されているとしましょう。すなわち1年後は ![]() 円、2年後は
円、2年後は ![]() 円、3年後は
円、3年後は ![]() 円・・・という具合です。
円・・・という具合です。
この場合、全ての配当を合算した現在価値は、割引率を ![]() とおくと
とおくと
![]()
となります。複雑に見えるかもしれませんが、これも等比数列の無限和に過ぎません。初項
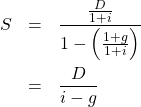
(2行目の変形は、分母・分子の双方に
次回は、毎年もらえる額が一定率で増えていくような「割賦」の計算です。
現在価値と割賦価値(7)インフレがある場合の割賦
