行列で表した分散公式
前回勉強した、「確率変数がn個ある場合の分散公式」。それを今回は行列で表してみます。行列で表すと、公式が覚えやすい、エクセルを使った計算が速くなる、ファイナンス理論への応用がしやすいなど、様々なメリットがあります。
結論を先に言えば、行列で表した分散公式は、「![]() 」という非常にコンパクトな表現になります(
」という非常にコンパクトな表現になります(![]() や
や ![]() の意味はこれから説明します)。今回の内容の基礎知識として、「行列の基本(16)二次形式の行列表現」を勉強してください。
の意味はこれから説明します)。今回の内容の基礎知識として、「行列の基本(16)二次形式の行列表現」を勉強してください。
確率変数が n 個あるとき、分散は n 個あります。共分散は確率変数のペアの数だけあります。それらを以下のように規則正しく並べたものを、「分散共分散行列 (Variance-covariance matrix)」と呼び、![]() で表します。
で表します。
分散共分散行列を作るときは、n 個の分散を左上から右下にかけて、対角線上に並べます。
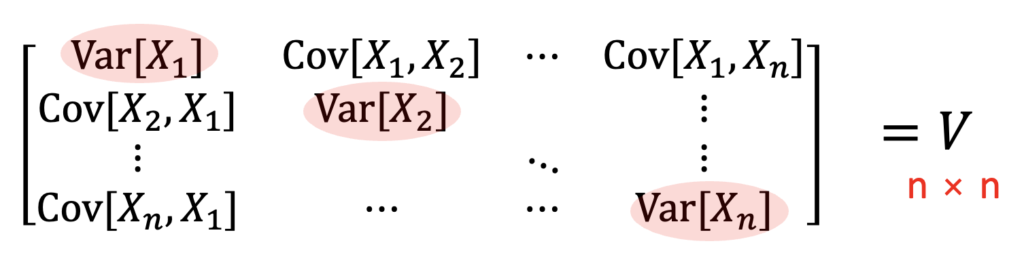
共分散は、例えば確率変数 ![]() と
と ![]() の共分散であれば1行2列目に、
の共分散であれば1行2列目に、![]() と
と ![]() の共分散であれば1行3列目に配置します。完成した分散共分散行列
の共分散であれば1行3列目に配置します。完成した分散共分散行列 ![]() は、n 行 n 列の行列です。
は、n 行 n 列の行列です。
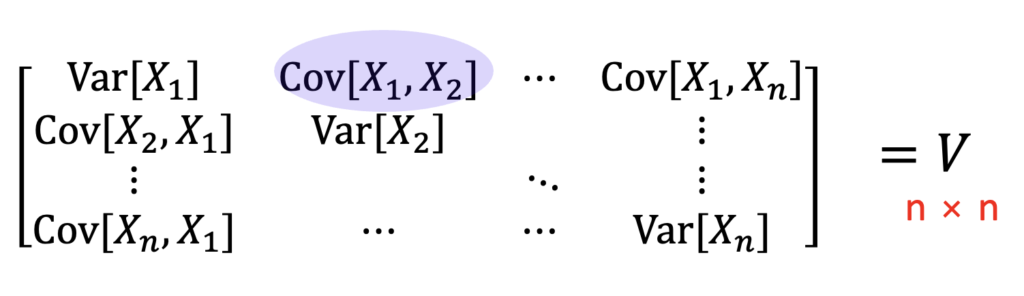
ちなみに、2つの確率変数の順番を入れ替えても共分散は同じ値です(![]() )ので、分散共分散行列は、対角線を軸に対称となっていることも知っておいてください。
)ので、分散共分散行列は、対角線を軸に対称となっていることも知っておいてください。
次に、n 個の確率変数の係数 ![]() をベクトルで表しておきます。縦に並べたものは
をベクトルで表しておきます。縦に並べたものは ![]() ,横に並べたものは
,横に並べたものは ![]() と表します。
と表します。
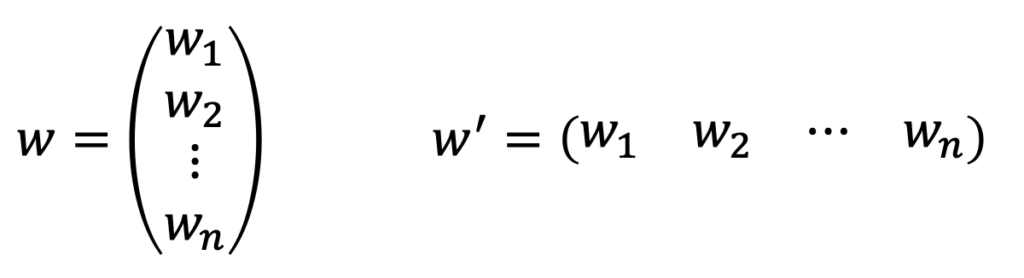
前回の分散公式は、![]() ,
, ![]() ,
, ![]() の掛け算で表すことができて、
の掛け算で表すことができて、
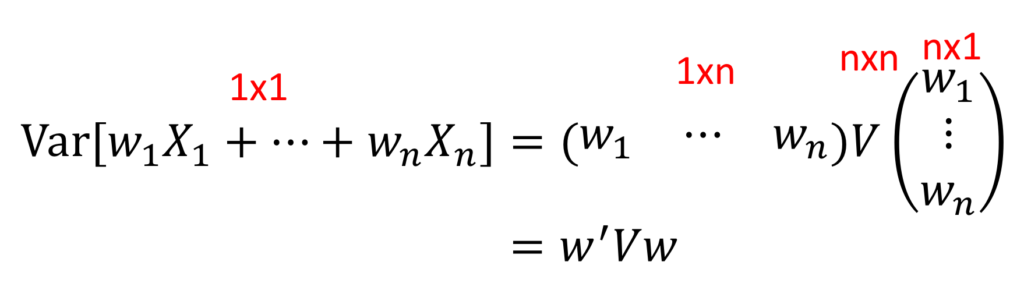
すなわち、単に ![]() となります。確率変数の線型結合の分散は、「係数を並べたベクトルで、分散共分散行列をサンドイッチしたもの」となるのです。
となります。確率変数の線型結合の分散は、「係数を並べたベクトルで、分散共分散行列をサンドイッチしたもの」となるのです。
それでは、以前も使った数値例で、この公式を使う練習をしてみましょう。
問題
確率変数が3つあり、それぞれ分散はVar(X)=131, Var(Y)=58, Var(Z)=24で与えられるとする。また共分散はCov(X, Y)=46, Cov(X, Z)=27, Cov(Y, Z)=15 で与えられるとする。
問1:分散共分散行列を作りなさい。
問2:![]() の分散を行列の掛け算で表しなさい。
の分散を行列の掛け算で表しなさい。
問3:行列の掛け算を実行して、分散を求めなさい。
(解答はこちら)
どうでしたか。これで分散公式の講義はおしまいです。分散公式は、ファイナンスの投資ポートフォリオ理論に応用されます。投資ポートフォリオの勉強の前に、しっかり頭に入れて、何も見なくても思い出せるようにしておきましょう。
解答(戻る)
問1
分散はX, Y, Zの順に対角線上に並べる。共分散は、Cov![]() を 第(1,2)成分と第(2,1)成分に、Cov
を 第(1,2)成分と第(2,1)成分に、Cov![]() を 第(1,3)成分と第(3,1)成分に、Cov
を 第(1,3)成分と第(3,1)成分に、Cov![]() を 第(2,3)成分と第(3,2)成分に配置する。よって
を 第(2,3)成分と第(3,2)成分に配置する。よって
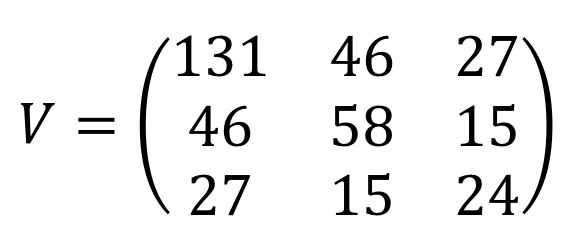
問2
公式中の ![]() は、0.2, 0.5, 0.3 を並べたものになるので、横に並べたものと縦に並べたものとで、分散共分散行列を挟めばよい。よって
は、0.2, 0.5, 0.3 を並べたものになるので、横に並べたものと縦に並べたものとで、分散共分散行列を挟めばよい。よって
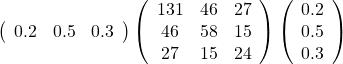
問3
行列のかけ算があやふやな人は、行列のかけ算1~5を参照のこと。行列のかけ算を実行すると
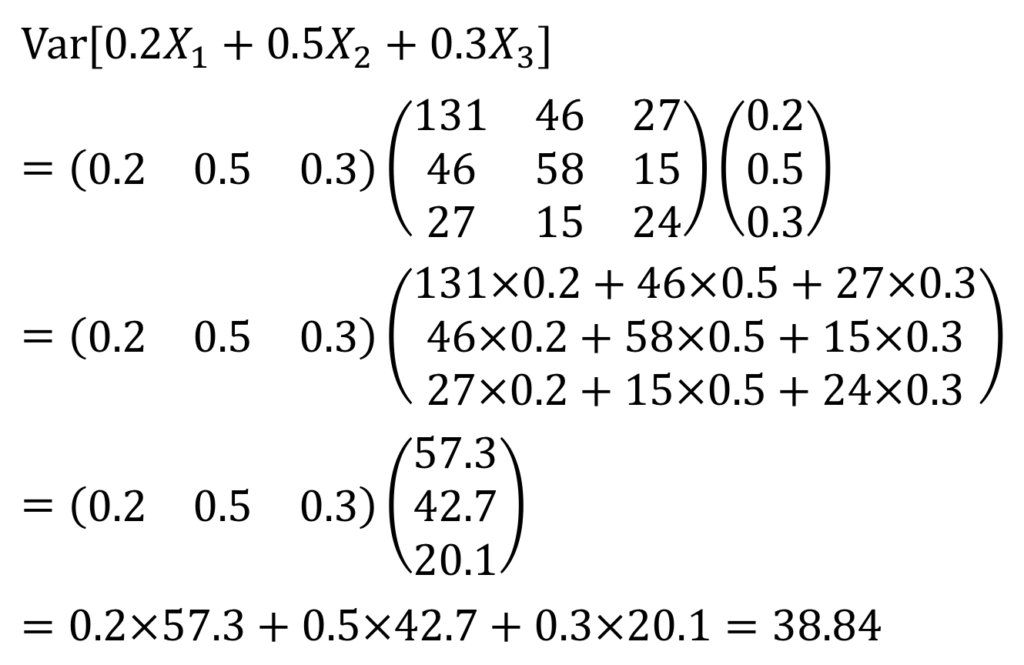
よって、求める分散は38.84となる。前々回の例題と、答えが一致しているはずである。
(問題に戻る)
