和の分散公式（４） | 午後はカフェで経済学

確率変数が３つの場合

前回は確率変数が X と Y の２つという設定で、線形結合の分散を求める公式を紹介しました。確率変数が３つ以上ある場合はどうでしょうか。２つだけのときより公式は長くなります。でも、理論の難しさは変わりません。今日は確率変数が３つある場合を勉強しましょう。

３つの確率変数 $X, Y, Z$ がある場合、それらの線型結合 $aX + bY + cZ$ の分散は、以下のようになります。ここでも、中高の数学で出てくる $(2x + 3y + 5z)^2$ のような式の展開との類推で覚えてください。

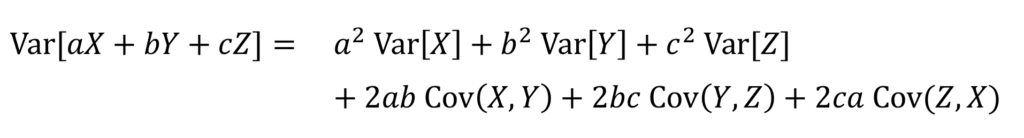
公式の右辺を見て下さい。まず３つの確率変数それぞれの分散の項があり、それらには係数の２乗がつきます。そのつぎに、共分散の項が続きます。確率変数のペアを全て列挙してください。ここでは $X$ と $Y$ ， $Y$ と $Z$ ， $Z$ と $X$ の３組ありますね。ペアが３組あるので、共分散も３つあります。それぞれの共分散には、２つの確率変数の前に付いていた係数を付け、２倍します。 $2ab$ などがそれです。

練習問題をしてみましょう。

問題
確率変数が３つあり、それぞれ分散は $\mbox{Var}(X)=131$ , $\mbox{Var}(Y)=58$ , $\mbox{Var}(Z)=24$ で与えられるとします。また共分散は $\mbox{Cov}(X, Y)=46$ , $\mbox{Cov}(X, Z)=27$ , $\mbox{Cov}(Y, Z)=15$ で与えられるとします。このとき $0.2X + 0.5Y + 0.3Z$ の分散を求めてください。

解答

$\begin{eqnarray*}&& \mbox{Var}[0.2X + 0.5Y + 0.3Z] \\\\&=& (0.2)^2\mbox{Var}[X] + (0.5)^2\mbox{Var}[Y] + (0.3)^2\mbox{Var}[Z] \\\\&& + 2(0.2)(0.5)\mbox{Cov}(X,Y) + 2(0.5)(0.3)\mbox{Cov}(Y, Z) + 2(0.2)(0.3)\mbox{Cov}(X,Y)\\\\&=& (0.2)^2 \times 131 + (0.5)^2 \times 58 + (0.3)^2\times 24 \\\\&& + 2(0.2)(0.5)46 + 2(0.5)(0.3)27 + 2(0.2)(0.3)15\\\\&=& 38.84\end{eqnarray*}$

確率変数が３つの場合が理解できれば、一般に n 個ある場合の公式も想像できるかもしれませんね。想像が合っているかどうか、次回チェックしてみましょう。

>> 和の分散公式（５）確率変数がn個の場合