X+Yの平均・分散・標準偏差
最後に、ビール屋とアイスクリーム屋を両方とも経営した場合の「合計の売上げ」である![]() の平均、分散、標準偏差を求めてみましょう。次の表では、
の平均、分散、標準偏差を求めてみましょう。次の表では、![]() の列、
の列、![]() の列のあとに、合計の売上げの列を付け加えてあります。合計の売上げは、「残暑」「普通」「寒い」の順に170万円 (17 JMY)、110万円 (11 JMY)、70万円 (7 JMY)です。
の列のあとに、合計の売上げの列を付け加えてあります。合計の売上げは、「残暑」「普通」「寒い」の順に170万円 (17 JMY)、110万円 (11 JMY)、70万円 (7 JMY)です。
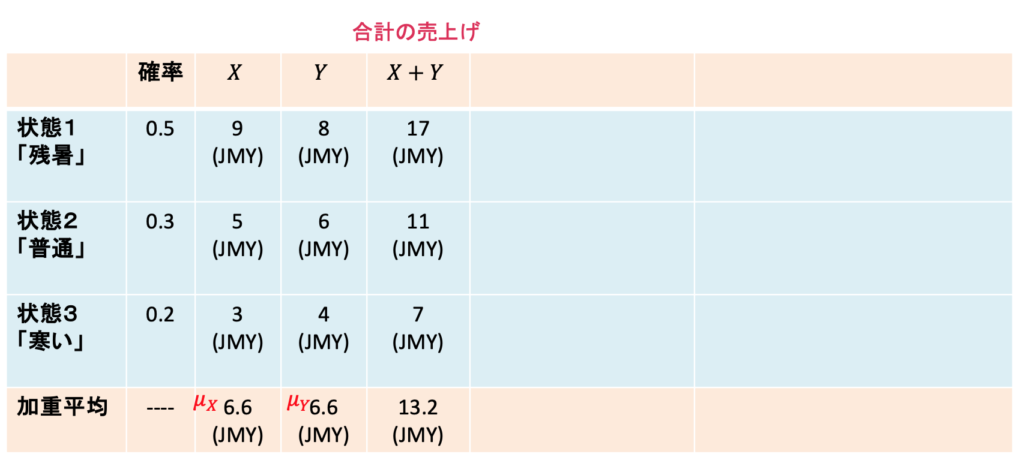
X+Yの平均(期待値)
平均は
![]()
あるいは
![]()
と求まります。
X+Yの分散
・まず、各状態における実現値から平均を引いた値の列を書き加え、
・次に、それを2乗した列を書き加え、
・最後に、確率を使って加重平均を求める
です。それを実行したのが次の表です。これで分散Var

X+Yの標準偏差
最後に、分散の平方根をとれば標準偏差![]() (JMY)となります。この標準偏差は、前々回に求めた、
(JMY)となります。この標準偏差は、前々回に求めた、![]() と
と![]() それぞれの標準偏差を足しても出てきません。
それぞれの標準偏差を足しても出てきません。![]() の標準偏差と、
の標準偏差と、![]() の標準偏差を足しても、
の標準偏差を足しても、![]() の標準偏差にはならないのです。ですが、その話は重要なので、「和の分散公式」のシリーズで改めて詳しく説明したいと思います。
の標準偏差にはならないのです。ですが、その話は重要なので、「和の分散公式」のシリーズで改めて詳しく説明したいと思います。
これでこのシリーズはひとまず終わりです。次回からは、複数の確率変数があるときの、期待値や分散について勉強します。
>> 期待値の基本性質(1)期待値の外に出せるもの、出せないもの
