確率変数の「平・分・共・標・相」（５）

共分散と相関係数

各天候状態におけるビール店とアイスクリーム店の業績を、もう一度ふり返ってみましょう。「残暑」「普通」「寒い」とき、ビールの売上げは順に90万円、50万円、30万円。アイスクリームの売上げは順に80万円、60万円、40万円。２つのビジネスはある意味「運命共同体」であることが見て取れます。結局、暑ければどちらも売れるし、寒ければどちらも売れません。統計的に言うと、２つの確率変数 $X$ と $Y$ は、同じ方向に連動 (co-movement) しているのです。

これと反対の例もあります。「輸入業」と「輸出業」がそれです。円高ならば輸入しやすく、輸出しにくい。逆に円安は、輸入にとってマイナス、輸出にとってはプラスです。つまり「輸出業」と「輸入業」の業績は、反対方向に動く傾向があると考えられます。

ビール店とアイスクリーム店の業績は同方向の連動で、輸入業と輸出業の業績は反対方向の連動。この、２つの確率変数の「連動性」とか「運命共同体である度合い」を数値化してくれる指標が、共分散と相関係数です。順序としてはまず共分散という中途品を計算し、最後の仕上げをして相関係数にします。

ステップ８
共分散を計算しましょう。まずは、以下の表のように、 $X-\mu_X$ の列と、 $Y-\mu_Y$ の列を掛け合わせて、最終列に書き込みます。

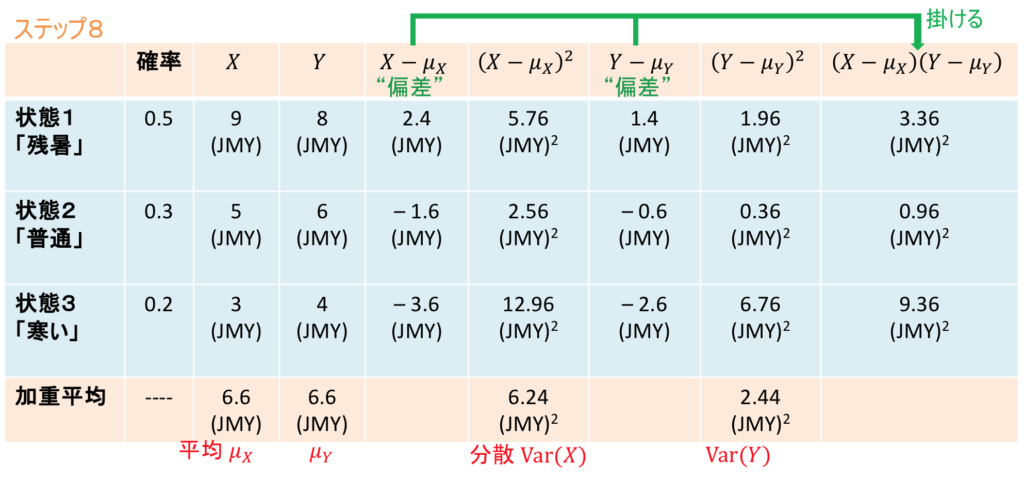
例えば「残暑」の場合、ビールの売上げの平均からの乖離は2.4 (JMY), アイスクリームの方は1.4 (JMY)ですから、その積は3.36 (JMY) $^2$ となります。（単位も機械的に掛け合わせてください。）「平均からの乖離」が $X$ も $Y$ も同じ符号のとき、この積はプラスになります。ビールが売れないときはアイスクリームも売れない、そんな２つの確率変数ならば、この積はプラスになりやすくなります。一方、輸出業が売れないときは、輸入業が売れる、そんな２つの確率変数ならば、この積はマイナスになりやすくなります。

ステップ９
最後に、この「乖離の積」に関して、確率0.5, 0.3, 0.2を使って加重平均を求めたものが共分散です。共分散 (Covariance) は、頭文字をとって $\mbox{Cov}(X, Y)$ と表します。式は

$\begin{eqnarray*}\mbox{Cov}(X, Y) &=& 0.5 \times 3.36 \mbox{ (JMY)}^2 + 0.3 \times 0.96 \mbox{ (JMY)}^2 + 0.2 \times 9.36 \mbox{ (JMY)}^2 \\&=& 3.84 \mbox{ (JMY)}^2\end{eqnarray*}$

です。表にも書き込んでおきます。

ここで、計算過程で２つの積を計算したせいで、単位が「十万円」の２乗になっていることに注意してください。分散と同様、共分散もイメージが湧きにくいという弱点があります。そこで、２つの変数の連動性の指標として、より広く用いられているのが相関係数です。

ステップ10
最後のステップとして、相関係数を求めましょう。相関係数は、ギリシア文字の $\rho$ (ロウ)を使って表します。 $X$ と $Y$ の相関変数を求めるためには、共分散を、前回求めた $X$ , $Y$ それぞれの標準偏差で割ります。つまり

$\begin{eqnarray*}\rho_{X, Y} = \frac{\mbox{Cov}(X,Y)}{\sigma_X \sigma_Y} = \frac{3.84 \;(\mbox{JMY})}{2.50\;(\mbox{JMY}) \;\; 1.56\;(\mbox{JMY})} = 0.984\end{eqnarray*}$

です。相関係数は必ず $-1$ と1の間の値になります。1であれば「正の完全相関」、 $-1$ であれば「負の完全相関」と言い、0であるときは $X$ と $Y$ は無相関だ、と言います。1や $-1$ に近ければ強く連動している、0に近ければあまり連動していない、というのですから、相関係数の大きさを見ればすぐ連動性の大きさがピンと来ますね。この例のビールとアイスクリームの売上げは、かなり相関が高いことが分かります。ほとんど運命共同体です。

どうでしたか。簡単な数値例で表を作って、ステップ１からステップ10まで、一つ一つ手順を確認しながら練習してみてください。次回は最終回です。ビールとアイスクリームの「合計の売上げ」について平均や分散を計算してみましょう。

>> 確率変数の「平・分・共・標・相」（６）X+Yの平均・分散・標準偏差