確率変数の「平・分・共・標・相」（３）

分散

前回は、お祭りにビール店とアイスクリーム店を出店するという設定で、ビールとアイスクリームそれぞれの売上げの期待値を計算しました。もう一度、前回の最後の表を見てみましょう。ビールもアイスクリームも売上げの期待値は66万円で同じなのですが、よく見るとビールの方がリスキーな商売であることに気づきます。暑ければビールは90万円も売れるのですが、寒いとたったの30万円しか売れません。一方、アイスクリームの方は、良くてもせいぜい80万円しか売れないのですが、悪くても40万円は売れるのです。

ビールに比べると、アイスクリームは手堅い感じがします。統計的な言い方をすると「ビールの売上げの方がばらつきが大きい」、経済学的な言い方をすると「ビールの売上げの方がリスクが大きい」とも言えますが、この「ばらつき」や「リスク」を測る指標が、「分散」と「標準偏差」です。分散は標準偏差を計算する過程で出てくる中途品で、順序としてはまず分散が求まり、それを標準偏差にします。

ステップ３
それではビールの売上げ $X$ の分散を求めてみましょう。以下の表「ステップ３」を見てください。まず、各状態における $X$ の実現値から、平均の6.6を差し引いた、“平均からの乖離” を求め、新しい列に書き入れます。平均からの乖離は、「偏差」と呼ばれます。

上の表で例えば2.4 (JMY)は、「残暑」だったときの売上げ 9 (JMY)が、平均6.6よりも2.4 (JMY) 高い、ということです。また、 $-3.6$ (JMY)は、「寒い」ときの売上げ3 (JMY)が、平均6.6よりも3.6 (JMY) 低い、という意味です。これが済んだら次のステップに進んでください。

ステップ４
今求めた、「それぞれの状態における（平均からの）乖離」を、それぞれ２乗して次の列に書き込みます。表「ステップ４」を見てください。

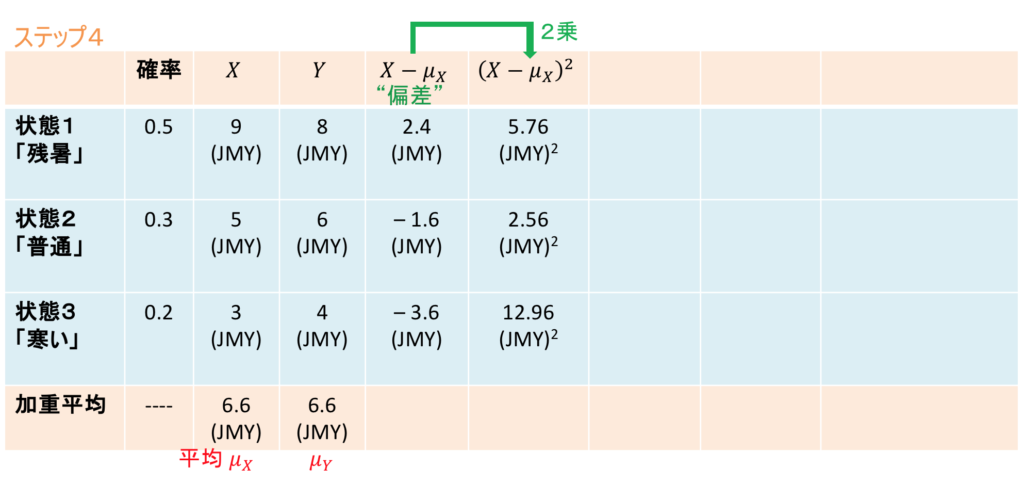
たとえば「残暑」のときの平均からの乖離2.4 (JMY)は２乗すると $(2.4 \mbox{ JMY})^2 = 5.76 \mbox{ (JMY)}^2$ となります。同様に、「普通」のときの $-1.6$ (JMY), 「寒い」ときの $-3.6$ (JMY)も２乗して書き込みます。分散を計算するときのコツは、計算途中で数字を２乗したときに、単位が何であろうと、単位も機械的に２乗しておくことです。

ステップ５
今求めた列の平均を、確率を使って求めます。答えは次の表にあるように、6.24 (JMY) $^2$ で、式は以下の通りです。

$\begin{eqnarray*} \mbox{Var}(X) &=& 0.5 \times 5.76 \mbox{(JMY)}^2+ 0.3 \times 2.56 \mbox{(JMY)}^2 + 0.2 \times 12.96 \mbox{(JMY)}^2\\ &=& 6.24 \mbox{(JMY)}^2 \end{eqnarray*}$

これが分散 (Variance)と呼ばれる値です。頭の３文字をとって $X$ の分散をVar( $X$ )と表します。直観的な説明はあとにするとして、まずは計算方法だけ、アイスクリームの売上げ $Y$ を使って練習しましょう。

ステップ６
アイスクリームの売上げの分散を計算します。手順は覚えていますか。まず、「残暑」「普通」「寒い」の各状態のときの $Y$ の値 8, 6, 4から、それぞれ平均 $\mu_Y=6.6$ を差し引いて「平均からの乖離」を求めて $Y-\mu_Y$ の列に書き込みます。次に、その結果をそれぞれ２乗して、 $(Y- \mu_Y)^2$ の列に書き込みます。最後に、確率0.5, 0.3, 0.2を使って加重平均を求めて、 $\mbox{Var}(Y) = 2.44$ $(\mbox{JMY})^2$ という答えが出てきます。それが次の表の「ステップ６」です。

分散を見ると、「ビールの売上げ」の方が6.24, 「アイスクリームの売上げ」の方が2.44なので、確かにビールの方が、ばらつき・リスクが大きいことが確認できました。

でも何だかピンと来ませんね。分散はピンと来ないのです。標準偏差ならもっとピンと来るはずです。次回はステップ７として、標準偏差を求めます。

>> 確率変数の「平・分・共・標・相」（４）標準偏差