内積計算のシグマ表示 その2
今回は、第4回「内積計算のシグマ表示 その1」の続きです。文字がたくさん出てきてもひるまないための訓練をします。
同じ長さのベクトルが2つあれば内積を計算できますが、今回はベクトルがたくさんある状況を考えます。
例えば、![]() が、それぞれ数字が
が、それぞれ数字が ![]() 個並んだベクトルとしましょう。つまり
個並んだベクトルとしましょう。つまり

そして、これらとは別に、やはり数字が
![]()
ここで、
まず、ベクトル
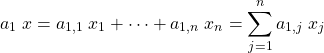
です。一般には
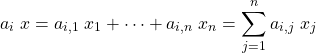
ということになります。
どうでしたか。このように、たくさんの文字が出てくることにも、少しずつ慣れていきましょう。
