和の記号シグマ（３） | 午後はカフェで経済学

次は、 $x_1, x_2, x_3, \cdots, x_{100}$ という数列に関してシグマ表記を使う勉強をしましょう。たとえば

をシグマで表すと、それぞれどうなるでしょうか。

１つめの「第100項まで足す」の正解はいろいろありえますが、

$\begin{eqnarray*}\sum_{i=1}^{100} x_i, \hspace{10mm} \sum_{i=1, \cdots, 100} x_i , \hspace{10mm} \sum_{1 \leq i \leq 100} x_i \end{eqnarray*}$

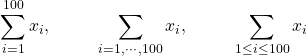
などでいいでしょう。もっとも、もとより100項しかないのなら、「1から100」と言うのは省略して、単に

$\begin{eqnarray*}\sum_{i} x_i \end{eqnarray*}$

とだけ書くこともあります。このように、 $i$ の範囲に指定がなければ、「全ての $i$ 」について足し合わせるのだと解釈されます。

次に、２問目の「２乗して足す」の正解は、

$\begin{eqnarray*}\sum_{i} (x_i )^2\end{eqnarray*}$

です。

$\begin{eqnarray*}\sum_{i} (x_i )^2=x^2_1 + x^2_2 + \cdots + x^2_{100}\end{eqnarray*}$

ですね。

最後に、３問目の「奇数番目だけ足す」の正解は

$\begin{eqnarray*}\sum_{i \mbox{~is odd}} x_i \end{eqnarray*}$

（oddは「奇数」の意味）と表すか、または

$\begin{eqnarray*}\sum_{i=1}^{50} x_{2i -1}\end{eqnarray*}$

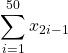
です。代入していけば

$\begin{eqnarray*}\sum_{i=1}^{50} x_{2i -1}=x_1 + x_3 + x_5 + \cdots + x_{99}\end{eqnarray*}$

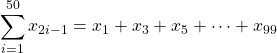
だと確認できます。

次回は「２つのベクトルの内積」を、シグマを使って表してみます。

>> 和の記号シグマ（４）内積計算のシグマ計算