舞台設定
表題の「平・分・共・標・相」は、それぞれ平均、分散、共分散、標準偏差、相関係数の頭文字です。統計学入門を勉強中の人は、すでに「確率統計の入り口」(3)-(5)で、確率変数の平均・標準偏差・相関係数を計算してみました。このシリーズでは、練習を通じて計算方法を復習しつつ、これらの概念の直観を身に付けましょう。
ファイナンスの現代ポートフォリオ理論を勉強中の人は、この５つを直観的に理解していると、あとあとの理解度が全然違ってきます。簡単な計算を通じて、これらの概念を一気にマスターしましょう。
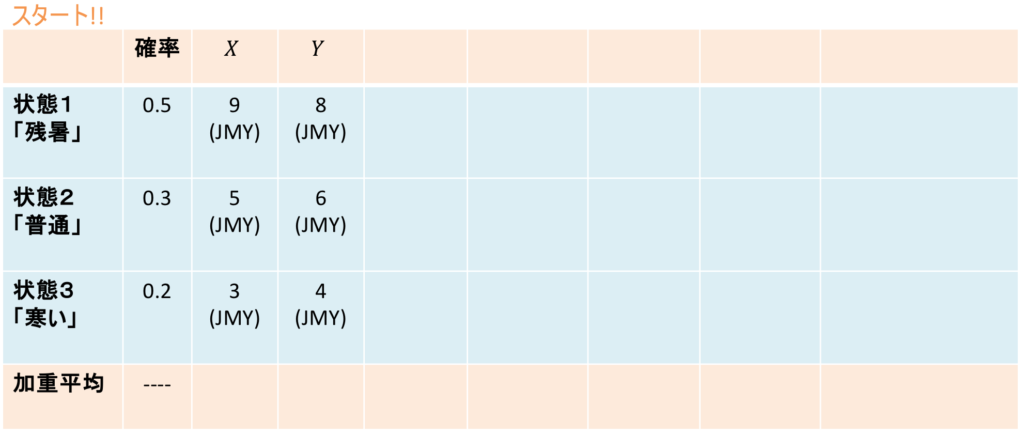
例として、あなたは９月に行われる秋祭りへの出店の準備をしているとしましょう。今年の９月は残暑が厳しいか、過ごしやすいか、それとも肌寒いか。長期天気予報では確率がそれぞれ0.5，0.3，0.2で表されているとします。次の「スタート!!」の表の最初の縦２列がそのことをまとめています。１列目は９月の気候の可能性として、「残暑」「普通」「寒い」の３つの状態があり得ることを表しており、２列目はそれぞれの確率を表しています。例えば「残暑」になる確率は0.5です。
例として、２つの確率変数 
と 
を考えます。あなたは秋祭りに「ビール店」を出店することにしていて、 はその売上げです。残暑が厳しければビールはバカスカ売れると分かっていて、売上げは90万円です。普通の気候ならばほどほどに売れて、売上げは50万円です。肌寒い気候だと、ビールはあまり売れず、30万円だろうと分かっています。表の３列目が、各状態におけるビール店の売上げ をまとめています。上の表では単位は「十万円」で、90万円は 9 JMYと略すこととします。JMYは「ジュウマンエン」の頭文字です。
もうひとつ、あなたは「アイスクリーム店」も出店することにしていて、 はアイスクリームの売上げだとしましょう。アイスクリームもやっぱり暑ければ売れる、寒ければ売れません。売上げは、残暑なら80万円 (8 JMY)，普通なら60万円 (6 JMY)，寒ければ40万円 (4 JMY) です。
舞台設定は頭に入りましたか。次回は手始めに と それぞれの平均を計算してみます。
>> 確率変数の「平・分・共・標・相」（２）平均（期待値）