無期限の割賦
前回の話を一般化すると、「1年後から毎年 ![]() 円支払うコンソル債」の割引現在価値は
円支払うコンソル債」の割引現在価値は
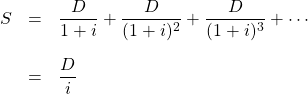
前回の例では
この公式を逆に使えば、現在価値から割賦価値を求めることができます。例えば、今1,000万円もらう代わりに、これから永久に毎年同額をもらうとしたら、それはいくらかというのが割賦価値です。
これは、別の視点から考えてみても、うなずける結果です。1,000万円を銀行に預金し、元金には手をつけずに金利収入だけを消費していれば、(金利1%の下では)毎年10万円を永久に消費できるからです。
このような無期限の割賦の概念は、「子孫との平等な分配」を考えるときにも応用できます。あなたの一族が先祖代々受け継ぐ土地があったとして、あなたがそれを1,000万円で売ってしまったとしましょう。売上げの1,000万円をあなたの代だけで使うのではなく、子孫代々と「平等に」分けようと考えたなら、あなたが使えるのは毎年10万円だけです。「半分は子孫のために預金しておく」というのでは、平等に分けたことにはなりません。全額預金して、毎年利息だけを使うというのが正しいのです。
19世紀、ロシアは国土の一部であるアラスカをアメリカに売却してお金を得ました。また、現在の自治体は、自分たちの土地に原発のゴミを受け入れてお金を得るという選択肢があります。そのようにして一括で受け取ったお金を、もし末代まで均等に配分するとしたら、各年いくら使えるか。それが(無期限の)割賦価値です。
次回は、受け取るお金が毎年一定率で上昇していく場合の割引現在価値を勉強します。
>> 現在価値と割賦価値(6)株式の割引現在価値
