ソロー・モデル３（考察編）
おさらいすると、ドーマー・モデルでは、貯蓄・投資をしていれば、経済は一定の成長率でずっと成長し続けました。一方のソロー・モデルでは、資本が少ないうちは急速に成長し、2，30年もすると成長は止まりました。
この違いは、生産関数の違いから来ています。ドーマーは、資本の量 
を増やせば、産出 
もそれに比例して増える生産関数を仮定しました。
一方のソローは、産出は資本と労働両方の関数であると仮定しました。
後者の場合、（労働を変えずに）資本の量だけ増やしても、産出は比例して増えはしません。グラフで表せば、次のような違いがあります。
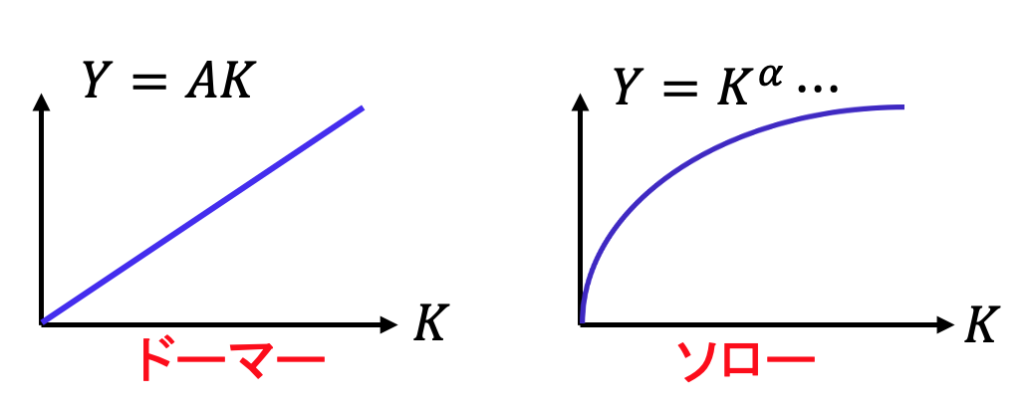
パソコンを使って生産をする企業を想像してください。ドーマー・モデルでは生産は単純にパソコンの台数に比例します。ですから、パソコンの数が２倍になれば生産も２倍、パソコンの数が100倍になれば生産も100倍です。
一方、ソロー・モデルでは労働者がパソコンを用いて生産します。100人の労働者がいる事業所で、パソコンが10台から20台に増えたら、生産は倍増するかもしれません。でも、10台から1000台になったからといって生産は100倍にはならないでしょう。パソコンに限らす、機械でも、車でも同じことです。
この「生産関数の違い」が、貯蓄・投資によって成長し続けるドーマー・モデルと、貯蓄・投資をしていても2，30年で成長が止まるソロー・モデルの違いとなって現れます。ドーマー自身も、のちにソローのモデルの方が良いと認めました。
それでは、先進国はどのようにして200年間成長し続けたのでしょうか。これに対するソローの答えは、「テクノロジーが進歩し続けたから」です。ソローのモデルでは、技術水準が成長率 
で増加します。
前回のシミュレーションでは、
と設定しましたが、試しに 
（年率0.4％）としてシミュレーションしてみましょう。その他の設定は前と同じです。
資本が希少なうちは急速に成長し、資本が十分蓄積されたあとは、一人当たりの生産や消費が一定率（年率0.4％）で成長しています。このように、ソロー・モデルにおける長期的な経済成長率は、テクノロジーの進歩のスピードに等しくなります。
ではテクノロジーを進歩させる（ の値を大きくする）にはどうすれば良いかという問いですが、 は外生パラメータですから、ソロー・モデルでそれに答えることはできません。ソロー・モデルでは、長期の経済成長率がどのように決まるかは分からないのです。
これで経済成長論の入門的な話は終わりです。引き続き経済成長論に興味のある人は、「経済成長理論・中級」のシリーズに進んでください。（未定）