>> 序，１，２，３，４，５，６，７，８，９，10，11

ソロー・モデル２（シミュレーション編）


今回は、ソロー・モデルをシミュレーションしてみます。前回出てきたソロー・モデルの差分方程式をまとめると、

    \begin{eqnarray*}Y_t &=& K_t^{\alpha} (A_tN_t)^{1-\alpha}\\C_t &=& (1-s) Y_t\\I_t &=& sY_t\\K_{t+1} &=& I_t +(1-\delta)K_t\\N_{t+1} &=& (1+n)N_t\\A_{t+1} &=& (1+g)A_t\end{eqnarray*}



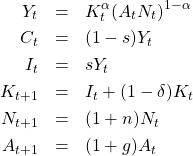
です。人口と技術水準の初項（N_1 と A_1）は、ともに１に基準化しましょう。資本に関しては、労働と比較して当初は少なめであると仮定し、K_1=0.1 としましょう。


次に、それ以外の外生パラメータを設定します。人口増加率をn=0.01（年率1％）とし、生産性 A_t の成長率は g=0（技術の進歩なし）とします。生産関数のパラメータは \alpha=1/3，資本減耗率は \delta=0.1，貯蓄率はs=0.1（10％）とします。


以下がシミュレーションの結果です。横軸が時間で、一人当たりの産出、消費、資本の量が時間とともにどう変わっていくかを表しています。


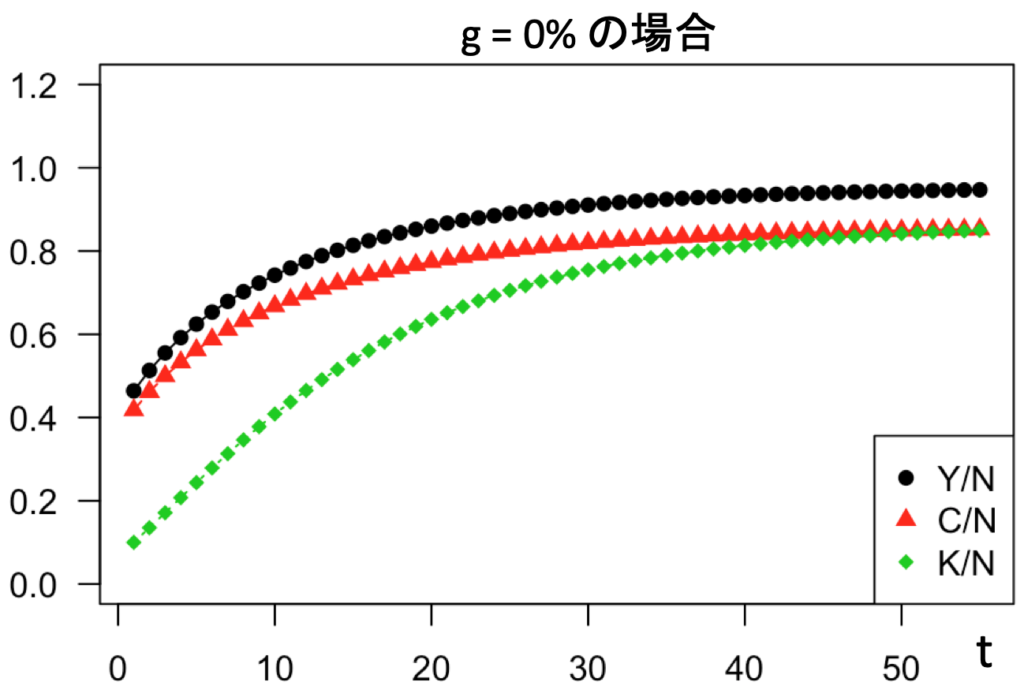
傾きが急なところが成長している期間、平らなところが成長していない期間に相当します。まず、最初の10年くらいは急速に成長していますが、これは当初少なかった資本が、徐々に蓄積されているからです。資本の蓄積が落ち着くにつれて成長は鈍り、そのうち止まってしまいます。このように、最初は高い成長率でも、最後は成長率がゼロになっているのがポイントです。


貯蓄率を上げてみたらどうでしょうか。ドーマー・モデルでは、「貯蓄率」が経済成長率を決める大事な要因でしたから、ソロー・モデルでも貯蓄率が大事かもしれません。そこで、ためしに貯蓄率 s を0.15（15％）に上げてシミュレーションしてみると


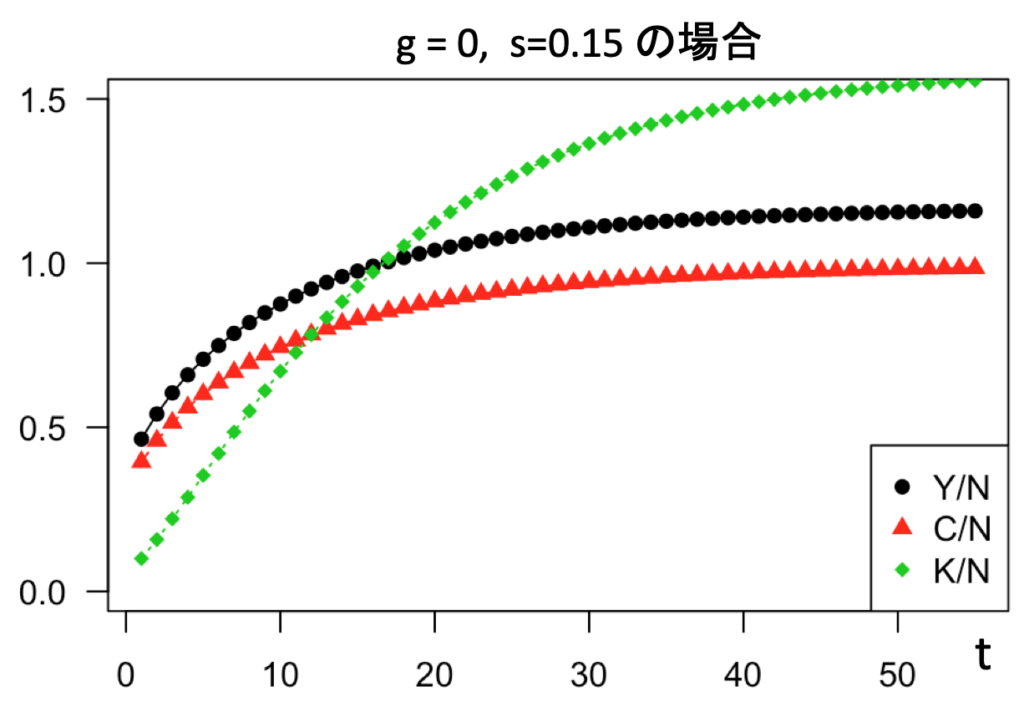
一人当たりの資本や産出が、さっきよりも高いところに収束していますが、やはり最終的に曲線は平らになっています。s=0.99（99％) にしても同じことです。30年もすると、経済成長率はほぼゼロとなります。いくら貯蓄率を大きくしても、将来的な成長率には貢献しないのです。


この結果は、ドーマー・モデルの結果とは対照的です。ドーマー・モデルでは、経済は30年でも50年でも、継続的に一定率で成長しました。そして、成長率を決めるのは貯蓄率でした。


どうしてこのような違いが生まれるのでしょうか。次回はドーマー・モデルとソロー・モデルを比較しながら、ソロー・モデルの示唆することを考えてみましょう。

>> 経済成長論（１１）ソロー・モデル３　考察編