>> 序，１，２，３，４，５，６，７，８，９，10，11

ドーマー・モデル２　インプリケーション編


前回はドーマー・モデルの差分方程式を導出しました。まとめると

    \begin{eqnarray*}Y_t &=& AK_t\\C_t &=& (1-s) Y_t\\I_t &=& sY_t\\K_{t+1} &=& I_t +(1-\delta)K_t\end{eqnarray*}


Y_t は産出、K_t は資本、C_t は消費、I_t は投資でした。A，s，\delta の３つはパラメータです。


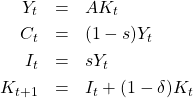
ドーマーの想定する世界では、経済成長率はどのように決まるのでしょうか。人口は一定と仮定して考えてみましょう。まず、「産出の成長率」は、「資本の成長率」と同じであることが示せます。

    \begin{eqnarray*}\frac{Y_{t+1}}{Y_t} = \frac{AK_{t+1}}{AK_t} = \frac{K_{t+1}}{K_t} \end{eqnarray*}


では資本はどのように成長していくかと言えば

    \begin{eqnarray*}K_{t+1} &=& I_t +(1-\delta)K_t\\&=&sY_t + (1-\delta)K_t\\&=& sAK_t + (1-\delta)K_t\\&=& (sA+1-\delta)K_t \end{eqnarray*}


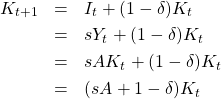
ですので、両辺を K_t で割ることにより、成長率は

    \begin{eqnarray*}\frac{K_{t+1}}{K_t} = 1 + (sA-\delta)\end{eqnarray*}


となります。一国の経済成長率は、３つのパラメータの値で決まることが分かります。


資本減耗率 \delta と、その国の生産効率性を表す A は、人々の意思で今すぐどうこう変えられる値ではありません。３つのパラメータのうち、意思で決められるのは貯蓄率 s です。つまり、上の式は「貯蓄率が経済成長率を決める」と言っています。今消費するのを我慢して、建物や機械に投資すれば、経済は成長するというのです。


たとえば仮に A=0.5，\delta=0.06 だとすると、
s=0.2 ならば経済成長率は0.04（4％）
s=0.3 ならば経済成長率は0.09（9％）
です。たくさん貯蓄（投資）すれば、それだけ速く成長します。アリとキリギリスの「アリ」であればあるほど、経済は速く成長していくというのが、ドーマー・モデルのメッセージです。


次回は、このモデルを現実に当てはめた経済学者たちの経験についてお話しします。

>> 経済成長論（８）ドーマー・モデル３　歴史編