二重のシグマ その3
前回の例を少し変えて、今回は、クラスごとに生徒の人数が異なる場合を考えましょう。
ひとクラスの人数が、1組から6組の順に、40人、38人、41人、39人、40人、41人であるとします。学年全員の点数の合計をシグマで表してみましょう。
手順としてはまず、各組の生徒の人数を表すベクトルを作ります。![]() 組の生徒数を
組の生徒数を ![]() で表すことにすれば、
で表すことにすれば、
![]()
です。すると、学年全員の点数の合計は
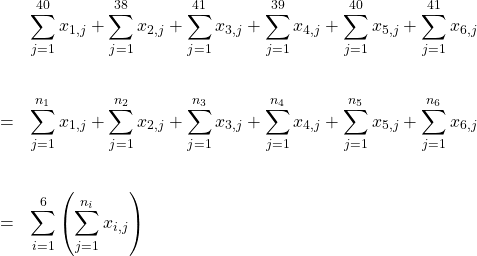
と表せます。1つめのイコールは、各組の生徒数を
前回のように表であらわしてみましょう。各組の生徒数が異なるため、行の終わりが揃っておらず、でこぼこしています。
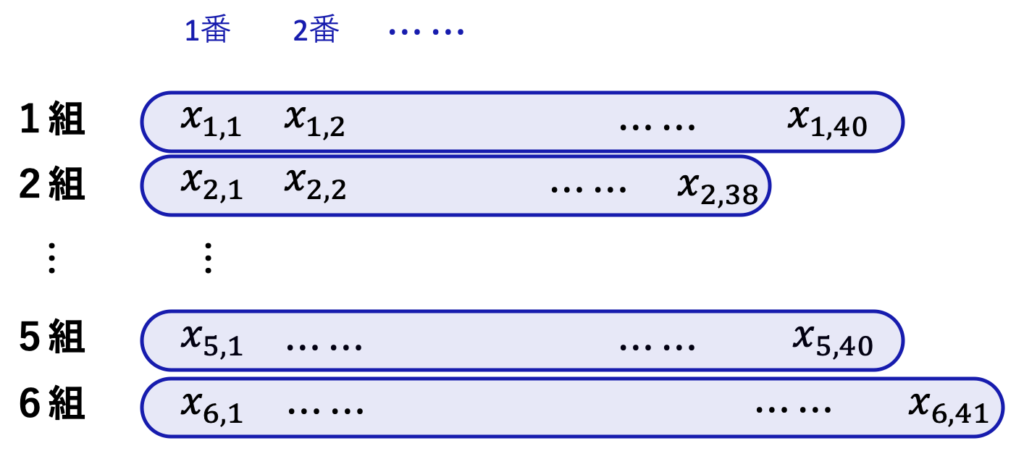
「まず横方向に足し」て合計を求めることは可能ですが、前回の例と異なり、「先に縦方向に足す」のは難しくなります。1列目は足せますが、41列目を足そうとしても、そもそも項が存在しない組があるからです。もしどうしても先に縦方向に足したければ、「データが無い所は0とみなす」などの強引な工夫がいります。例えば ![]() などとして、全ての組でいちおう41個データがあることにすれば、表はきちんとした長方形の形になり、縦方向に足すことも横方向に足すこともできるでしょう。
などとして、全ての組でいちおう41個データがあることにすれば、表はきちんとした長方形の形になり、縦方向に足すことも横方向に足すこともできるでしょう。
そうでもしない限り、終わりがでこぼこしているデータで、シグマ記号の順序を自在に変えることはできません。終わりが揃っていなくても、シグマ記号の順序を変えられる場合もありますが、それはちょっと難しいので、いずれ必要になったときに勉強しましょう。
次回は、「内積計算のシグマ表示(第4回)」を発展させます。文字がたくさん出てきても混乱しないように訓練することがねらいです。
>> 和の記号シグマ(9)内積計算のシグマ表示 その2
