二重のシグマ その2
今回は、前回の最後に出てきた、シグマ記号が二重になったケースを発展させていきたいと思います。
今回は、クラスの数は6つあって、それぞれのクラスに40人の生徒がいるとしましょう。そして、![]() 組の、出席番号
組の、出席番号 ![]() 番の生徒の点数が
番の生徒の点数が ![]() で表されているとします。たとえば
で表されているとします。たとえば ![]() ならば、2組・30番の生徒の点数です。
ならば、2組・30番の生徒の点数です。
添え字が2つあるデータは、表の形で考えると理解しやすくなります。以下の表では、点数のデータが、組は上から下に6行、出席番号は左から右に40列つかって並べられています。

このように数字を縦横に並べたとき、数学では横方向を「行 (row)」、縦方向を「列 (column)」と呼ぶので覚えてください。この例は6行、40列の表です。行は「ノートの行」、列は「朝礼の列」と覚えると、縦横が覚えやすいです。
全員の点数の合計は、シグマ記号を使ってどう表せばいいでしょうか。表し方は1つではありません。たとえば
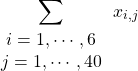
とか、
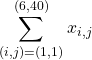
と表せます。これで、
さて、ここからが今日の本題です。実は、2つのシグマを使って、足し算する順番を指定することもできるのです。まず各組で40人の合計点を求め、そのうえで6組分足す、というのであれば、
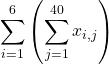
となります。内側のシグマ記号は、各
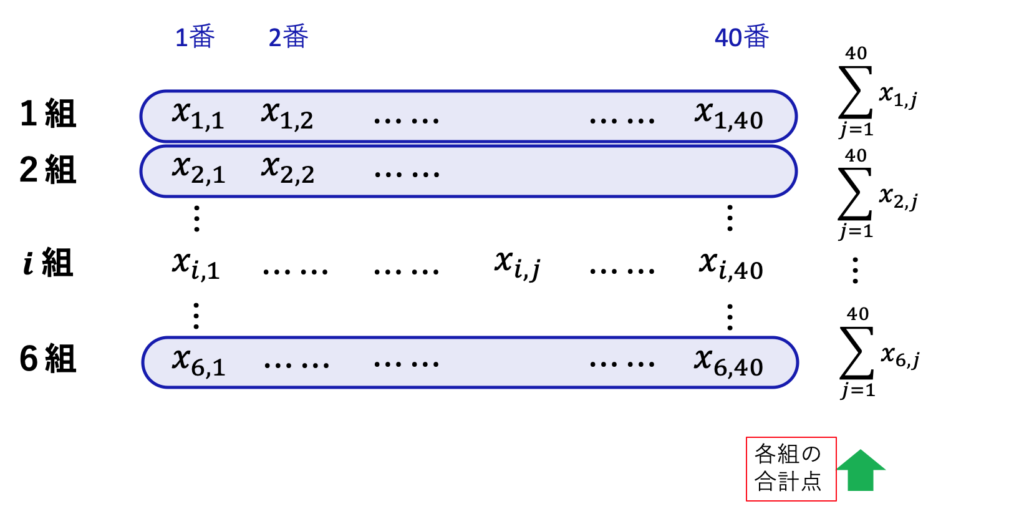
そのうえで、各組の合計点を合算しているのです。
一方、シグマの順序を入れ替えて
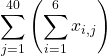
としたらどうでしょうか。この場合は、内側のシグマは、クラスは異なるが出席番号が同じ6人の合計をまず求めています。出席番号が1番の6人の点数の合計、出席番号が2番の6人の点数の合計・・・といった具合に、40個の合計点が求まります。その後、外側のシグマ記号にしたがい、その40個の数字を合計します。表でいうと、まずは各列の合計を求めていることになります。
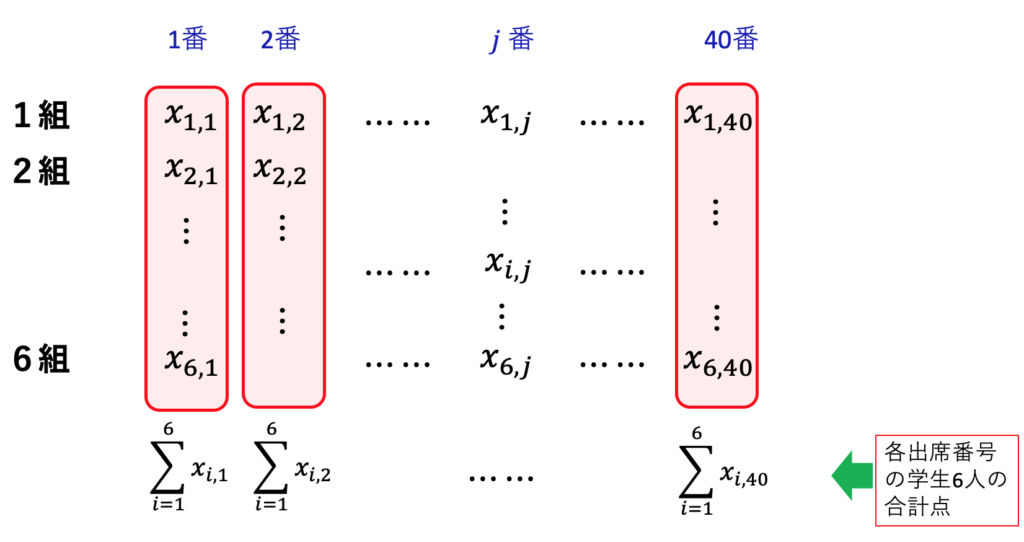
添え字が2つある場合の二重のシグマの意味は分かってきたでしょうか。次回は、クラスごとに生徒の人数が異なる場合を考えましょう。
>> 和の記号シグマ(8)二重のシグマ その3
