二重のシグマ その1
今回は、和のシグマ記号が二重になっているケースを勉強していきます。
ある学校には1組と2組のふたクラスあり、それぞれ40人の生徒がいます。1組の40人のテストの点数を
![]()
と表しましょう。添字の1つめが組、2つめが出席番号です。2組の40人のテストの点数も同じように
![]()
と表します。2組なので、最初の添字が全て2となっています。1組の点数の合計はシグマを使って表すと、
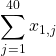
同様に、2組の点数合計は
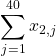
となります。したがって、1組・2組あわせた合計は
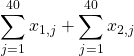
です。第1項が1組、第2項が2組です。ふた組だけの和ですが、これもシグマを使って表せば
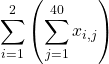
となります。シグマ記号が二重になってびっくりした人もいるかもしれませんが、最後の式から1つ前の式に戻るのは難しくありません。シグマ記号の意味にしたがい、
次回はこれを発展させて、シグマ記号が二重になるケースの理解を深めます。
>> 和の記号シグマ(7)二重のシグマ その2
