<< １，２，３，４，５，６，７，８，９

「何を足すのか」を明確にする

今回のポイント
和のシグマ表記の目的は「何を足すのか」を明確にすることである。明確であれば表記のしかたは柔軟である。



シグマ記号を使うと、長い規則的な足し算を、少ない労力で書くことが可能です。しかし、労力の節約のためだけなら、シグマを使わなくても、点々（\cdots）を使って、
「4+ \cdots + 12」とか、「3^2 + \cdots + 7^2」と表すこともできなくはありません。慣れない記号を使わなくても済む気がします。


足し算を「\cdots」を使って表すのが万能でない理由は、意味が読み手に伝わりにくくなる可能性があることです。たとえば

    \begin{eqnarray*}2 + 4 + \cdots + 16\end{eqnarray*}


はどういう意味でしょうか。

    \begin{eqnarray*}2 + 4 + 6 + 8 + 10 + 12 + 14+ 16\end{eqnarray*}


という、「偶数だけ足す」の意味かもしれないし、

    \begin{eqnarray*}2 + 4 + 8 + 16\end{eqnarray*}


という、「倍々しながら足す」の意味かもしれません。「\cdots」には、「私の意図を読んで！」という書き手の願いが込められており、何を足したら良いのかが、時として曖昧です。


その点、シグマ記号を使うと、前者は

    \begin{eqnarray*}\sum_{i=1}^8 2i \end{eqnarray*}

後者は

    \begin{eqnarray*}\sum_{i=1}^4 2^i \end{eqnarray*}


となり、読み手にとっての曖昧さがなくなります。その分書き手は、何をどういうルールで足していくのかを、しっかり意識しなければならないのです。


シグマ記号は、何を足すのかが明確であれば、どのような書き方をしても構いません。足し算の終点をシグマの上に書かなければならないという決まりもありません。例えば、上記の和は

    \begin{eqnarray*}\sum_{i=1,2,3,4} 2^i \end{eqnarray*}



    \begin{eqnarray*}\sum_{i=1,\cdots,4} 2^i \end{eqnarray*}



    \begin{eqnarray*}\sum_{1 \leq i \leq 4} 2^i \end{eqnarray*}



    \begin{eqnarray*}\sum_{i \in \{1,2,3,4\}} 2^i \end{eqnarray*}


などとしてもよいです。何をどの範囲で足すのかが伝わればいいのです。


練習問題を１つやってみましょう。「4から20までの偶数だけを２乗して足し合わせる」ということを、4^2 + 6^2 + \cdots + 20^2 と曖昧に書くのではなく、シグマ記号を使ってはっきり表してみてください。


これも、意味がはっきりしていれば、書き方はいろいろあります。もっともストレートな答えは


でしょう。あるいは、ダミー変数の方では偶数に限定せず、シグマの中で２倍して偶数にする方法もあります。その場合は

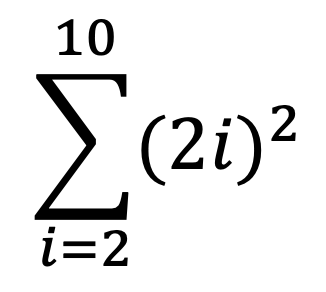
です。


次回は x_1, x_2, x_3, \cdots, という数列の和を、シグマ表記してみましょう。

>> 和の記号シグマ（３）数列の項の足し算