ダミー変数
今回のポイント
和のシグマ記号に出てくる ![]() や
や ![]() などの文字は、代入によって消えてしまう「ダミー変数」である。
などの文字は、代入によって消えてしまう「ダミー変数」である。
このシリーズでは、高校で習う![]() 記号を、経済学に必要なポイントに絞って勉強します。規則的な足し算は、ギリシア文字の大文字のシグマ
記号を、経済学に必要なポイントに絞って勉強します。規則的な足し算は、ギリシア文字の大文字のシグマ ![]() を使って表すことができます。たとえば、
を使って表すことができます。たとえば、
![]()
は、「![]() に4から12まで代入して足し合わせる」という意味になります。つまり、
に4から12まで代入して足し合わせる」という意味になります。つまり、
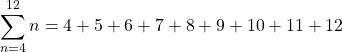
です。左辺は右辺と意味の上では同じですが、書くスペースが小さくて済みます。高校では、「足し算の出発点 ![]() をシグマの下に、終点
をシグマの下に、終点 ![]() をシグマの上に書く」と教わりますが、行間の都合上、文中では
をシグマの上に書く」と教わりますが、行間の都合上、文中では ![]() のようにシグマ記号の右に書くこともあります。
のようにシグマ記号の右に書くこともあります。
文字として、必ずしも![]() を使う必要はありません。
を使う必要はありません。![]() でも
でも ![]() でもハートマークでも同じです。
でもハートマークでも同じです。
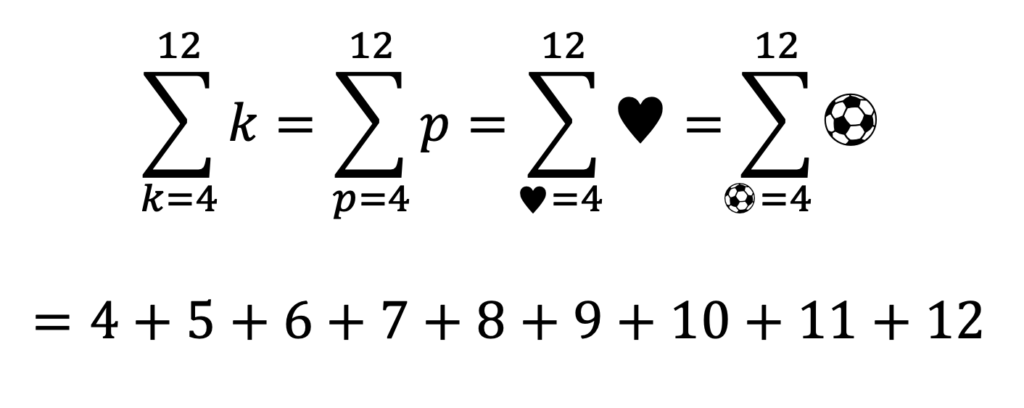
どんな文字を使っても等しい理由は、どのみち代入によって消えてしまう仮の変数に過ぎないからです。シグマ記号の中だけで有効なダミーという意味で、「ダミー変数」と呼ぶこともあります。![]() は文字式かもしれませんが、
は文字式かもしれませんが、
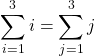
は文字式ではありません。![]() と言っているだけです。シグマ表記のダミー変数は、代入のための便宜上の文字に過ぎないことを覚えておいてください。
と言っているだけです。シグマ表記のダミー変数は、代入のための便宜上の文字に過ぎないことを覚えておいてください。
シグマ表記に慣れるため、もうひとつ、整数の2乗和の例を見てみましょう。次の、
![]()
は、どんな和でしょうか。シグマ記号の意味は「代入して足し合わせる」でしたね。ですからこれも、![]() に3を入れ、次に4を入れ・・・と次々に代入しながら足していきます。したがって、これは
に3を入れ、次に4を入れ・・・と次々に代入しながら足していきます。したがって、これは
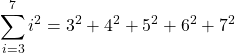
に等しくなります。
整数の和に関しては、次の公式が知られています。
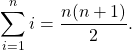
例えば ![]() であれば「1から10まで全部足すと55になる」ことを意味し、
であれば「1から10まで全部足すと55になる」ことを意味し、![]() であれば「1から20まで全部足すと210になる」ことを意味します。ここでは
であれば「1から20まで全部足すと210になる」ことを意味します。ここでは ![]() はダミー変数ですが、
はダミー変数ですが、![]() はダミー変数ではないことに注意しましょう。実際、右辺において
はダミー変数ではないことに注意しましょう。実際、右辺において ![]() は消えてしまっていますが、
は消えてしまっていますが、![]() はしっかり残っています。
はしっかり残っています。
さて、足し算をシグマ表記すると書くスペースが小さくて済むといいましたが、スペースの節約がシグマ表記の一番の目的ではありません。シグマ表記の本当の目的は、「何を足すのか」をはっきり示すことです。次回はそれを説明します。
>> 和の記号シグマ(2)「何を足すのか」を明確にする
