平均(期待値)
それでは、舞台設定ができあがったところで、まず![]() の平均(期待値)を求めましょう。以下の「ステップ1」の表をごらんください。
の平均(期待値)を求めましょう。以下の「ステップ1」の表をごらんください。
ステップ1
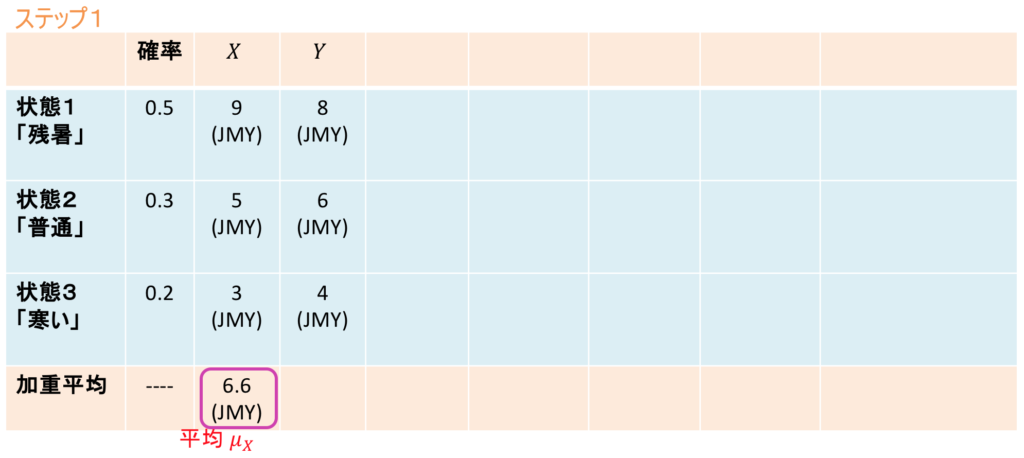
平均は、![]() の各実現値(ここでは9, 5, 3 JMY)に、対応する確率 0.5, 0.3, 0.2をそれぞれ掛けて、最後に合算することで求めます。平均は英語で mean なので、その頭文字mをギリシア文字の
の各実現値(ここでは9, 5, 3 JMY)に、対応する確率 0.5, 0.3, 0.2をそれぞれ掛けて、最後に合算することで求めます。平均は英語で mean なので、その頭文字mをギリシア文字の![]() (ミュー) を使って表します。したがって
(ミュー) を使って表します。したがって
![]()
となります。
「平均」ということの意味は「将来起こる
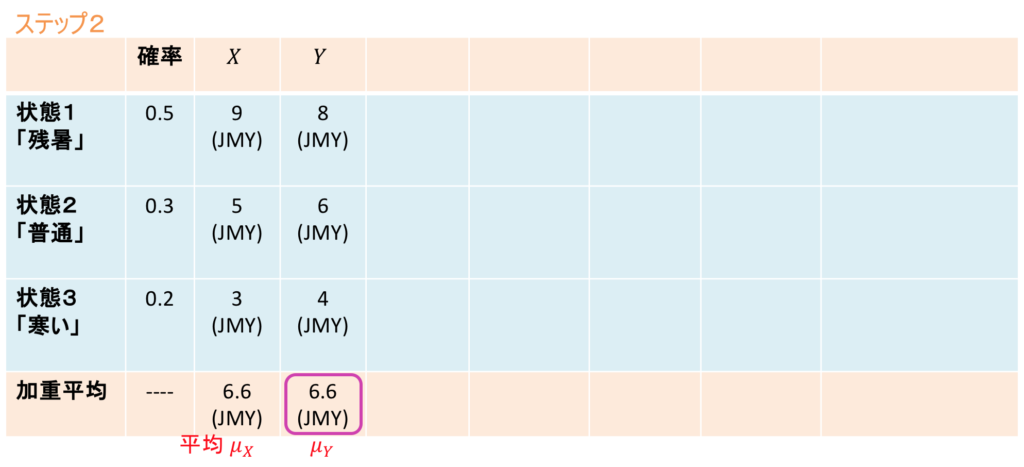
ステップ2
同じように、アイスクリーム店の売上げ
どうでしょう、できましたか?
式は
![]()
です。今回の例では、ビールの売上げとアイスクリームの売上げの平均は、たまたまどちらも同じ6.6 JMY (66万円) となっています。さあ、次は分散と標準偏差です。
>> 確率変数の「平・分・共・標・相」(3)分散
