解釈・用途
今日のポイント
最終利回りの解釈は、「もしイールド・カーブが平らだったら金利はいくつか」である。
最終利回りの用途は、満期やクーポンレートが様々な債券を比較することである。
前々回の数値例では、市場の金利は１、２、３年物の順に3％、4％、6％という設定でした。市場の金利は年限によって異なります。言い換えれば、イールド・カーブは平らではありません。
一方、「最終利回り」の定義は、金利が年限によらず 
に等しいかのようにみなして、１つの債券の価格からその を計算します。そのため、最終利回りを計算すると、各年限の金利の中間的な値が出てきます。
前々回の例では、最終利回りは債券Aが5.63％、債券Bが3.33％、債券Cが3.95％でした。１年目のキャッシュフローが多い債券であれば3％に近くなりますし、３年目のキャッシュフローが多い債券であれば6％に近くなります。特に、クーポンの無い「割引債」の場合は、最終利回りはその年限の金利です。この例では、３年物の割引債なら最終利回りはぴったり6％です。
実際のマーケットも見てみましょう。Bloombergの公表によれば、2020年10月9日における日本国債の利回りは以下のようになっています。
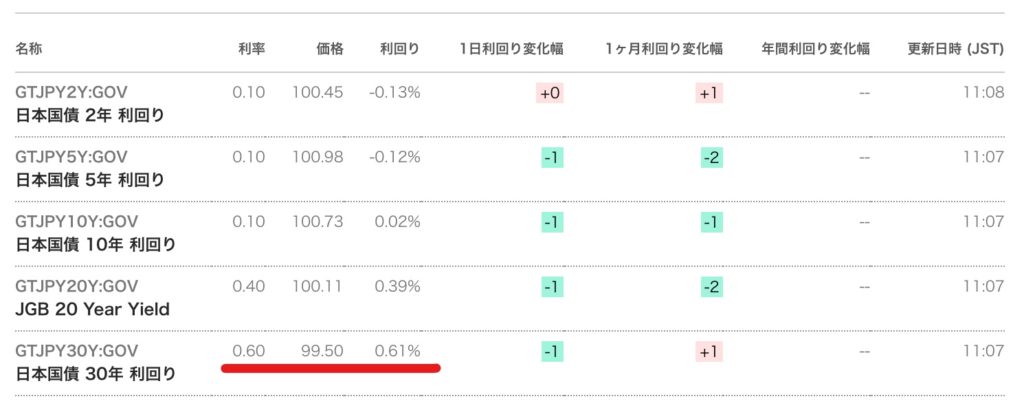
１列目に銘柄名が並んでいます。上から満期2年、5年、10年、20年となっており、一番下の行が満期30年の国債です。「利率」が0.60というのはクーポン・レートのことです。額面100万円であれば、毎年0.6万円、つまり6000円がクーポンとして支払われる債券です。次の「価格」99.5は、額面100当たりの価格です。額面100万円であれば、この日の価格は99万5000円ということになります。その次の「利回り」というのが最終利回りのことで、この日は0.61％となっています。
この図が示すように、最終利回りは債券ごとに異なります。そして、満期やクーポン・レートが異なる様々な債券を比べる１つの参考になります。しかしあくまで参考です。最終利回りさえ高ければいい、というわけではありません。キャッシュフローをもらえるタイミングも投資家にとっては大事です。例えば、１年物より３年物の金利の方が高いからと言って、「１年物より３年物の割引債が全ての人にとっていい」とはなりませんよね。１年間だけ投資したい短期の投資家もいます。
さて、この最終利回りは、「債券価格の変動」を分析・予測するために応用されます。次回はその話です。
>> 最終利回り（５）債券価格の変化