対数目盛りのグラフ1
掛け算的に変化する変数の場合は、グラフの描き方も気をつけなければなりません。
例として、2つの国の「外国人観光客数の推移」を比較する状況を考えてみましょう。ここで、A国は人口の少ない国、B国は人口の多い国であるとします(例えばポルトガルと中国など)。A国は当初の観光客数は1万人で、毎年10%ずつ増えていったとします。一方のB国は当初は観光客数が10万人で、毎年5%ずつ増えていったとします。両国の観光客数の推移は、以下の表の通りです。(単位は万人)
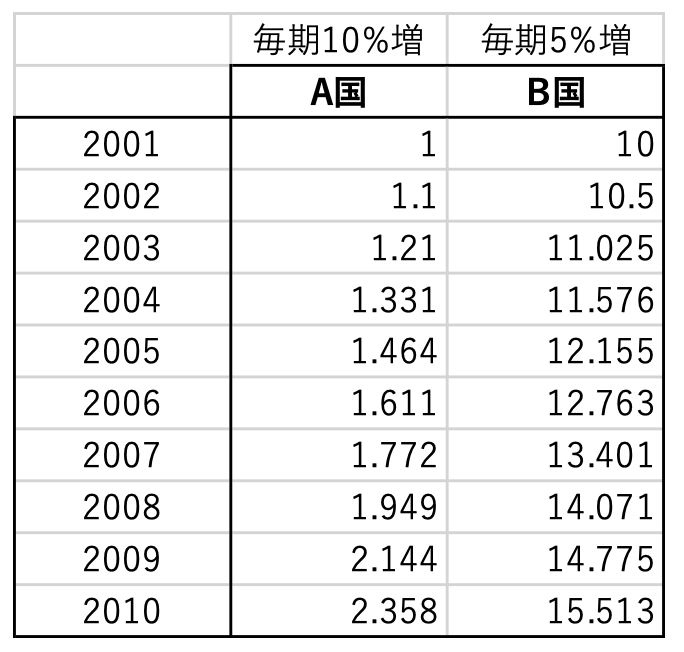
これをそのまま、横軸に「時間」を、たて軸に「観光客数」を取って図示すると以下のようになります。A国とB国のどちらの方が、観光客数の増加が激しいと感じるでしょうか。
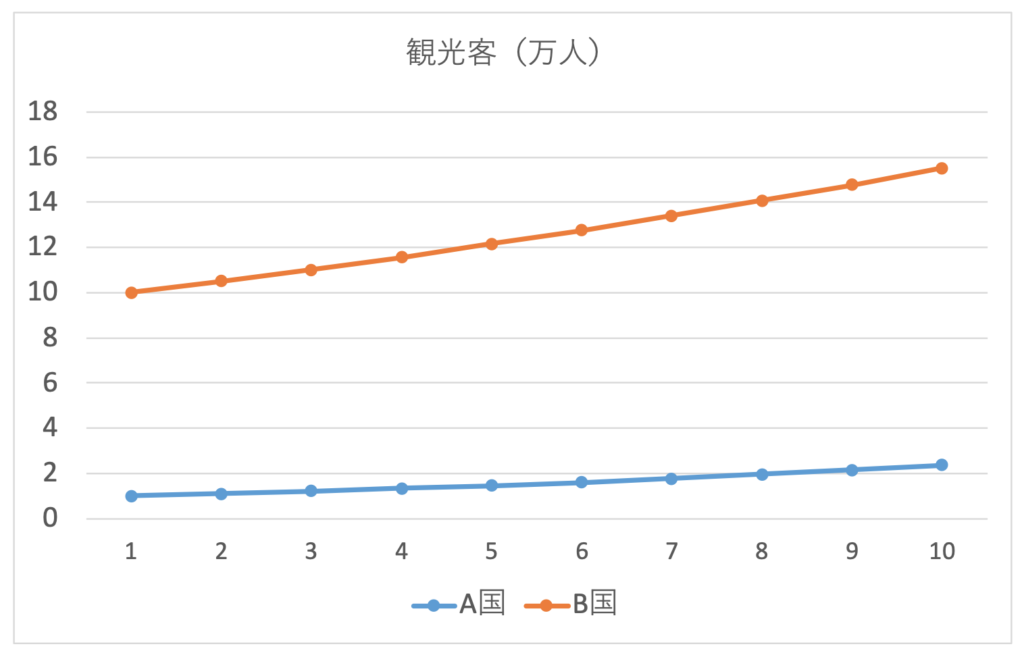
A国(青色の線)は毎年10%の増加、B国(朱色の線)は毎年5%の増加ですから、実際にはA国の方が急速に増えているのですが、グラフからはそんな感じがしません。原因は元々の水準の違いです。A国は最初1万人からスタートするので、初年度は1000人の増加です。対するB国は最初10万人からスタートするので、初年度は5000人の増加です。たて軸を単純に人数とすると、どうしても5000人の増加の方が大きな増加として表されてしまいます。
これを解決するには、「対数目盛り」を使います。たて軸は相変わらず観光客数なのですが、目盛りの取り方を、1, 2, 4, 8, というふうに等倍で取るのです。このように目盛りの取り方を変えると、同じデータでもずいぶん違ったグラフになります。
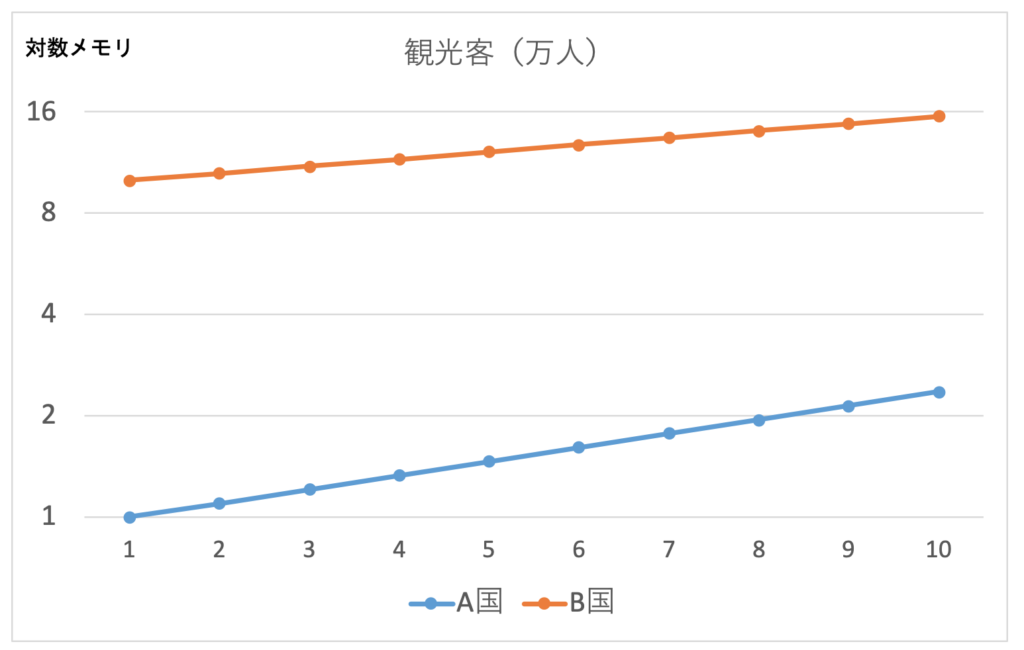
この図だと、元々が1万人であろうが、10万人であろうが、1目盛り上がるには2倍にならなければなりません。毎年10%で増えるA国の方が速く2倍になりますから、グラフの傾きも急になるのです。ちなみに、1目盛りにつき「2倍」である必要はありません。次の図では、1目盛りあたり「10倍」というふうに目盛りを取った図です。
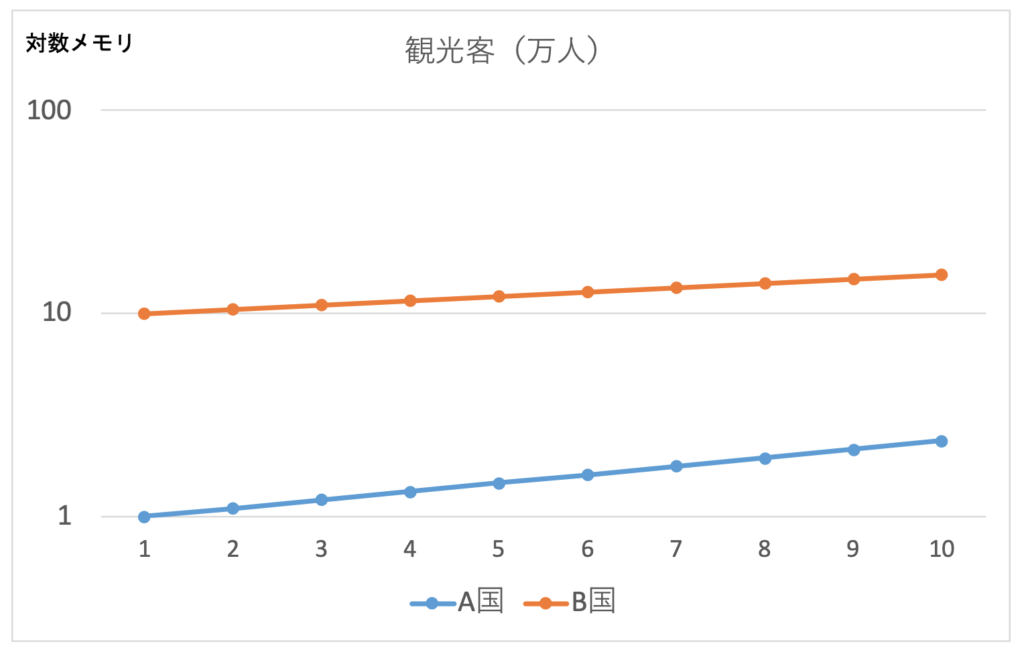
対数目盛りでは、たとえば2と4の中間点は3ではなく、![]() となります。1と10の中間点は
となります。1と10の中間点は ![]() です。
です。
このように、「年◯◯%」のようにかけ算的に変化していく変数の推移を図示するときは、たて軸に対数目盛りを使うことを検討しましょう。対数目盛りを使うことの大切さを理解するため、次回はもう一つ例を示したいと思います。
>> かけ算的に変化する変数(4)対数目盛りのグラフ2
