最大化(2変数・制約あり)
前回までは、制約条件の無い最適化問題を考えました。しかし、現実の最適化問題には、しばしば時間や予算などの制約があります。そこで今回は、制約条件つきの最大化問題をソルバーで解いてみましょう。
今回最大化する目的関数は、 ![]() です。これを
です。これを ![]() ,
,![]() について最大化します。
について最大化します。![]() と
と ![]() はどちらも正の数であるとします。制約は、
はどちらも正の数であるとします。制約は、 ![]() という不等式にしましょう。この制約のせいで、
という不等式にしましょう。この制約のせいで、![]() ,
,![]() を際限なく大きくすることはできません。
を際限なく大きくすることはできません。
この問題を正式に書くと以下のようになります。maxの右側に、最大化したい目的関数を書きます。maxの下には ![]() ,
,![]() と書いてありますが、これが「
と書いてありますが、これが「![]() ,
,![]() について最大化する」という意味です。また、制約は「s.t. 」に続けて書く決まりです。s.t. は subject to… (~の制約下で)の頭文字です。
について最大化する」という意味です。また、制約は「s.t. 」に続けて書く決まりです。s.t. は subject to… (~の制約下で)の頭文字です。
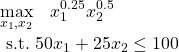
まずエクセルに式を入力します。
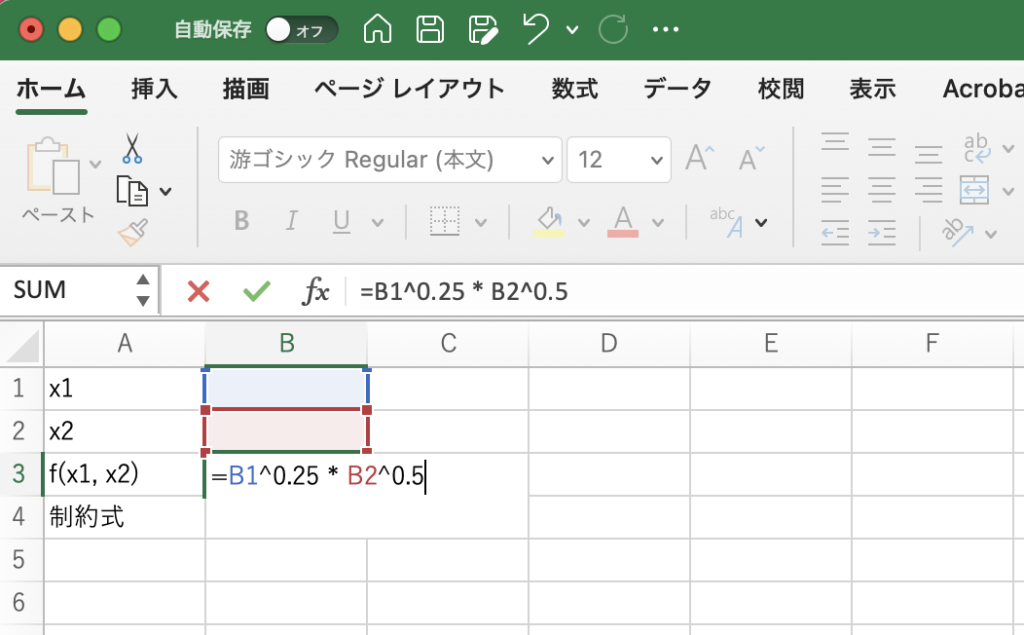
次に、制約式の左辺 ![]() を、セルB4に入力します。
を、セルB4に入力します。
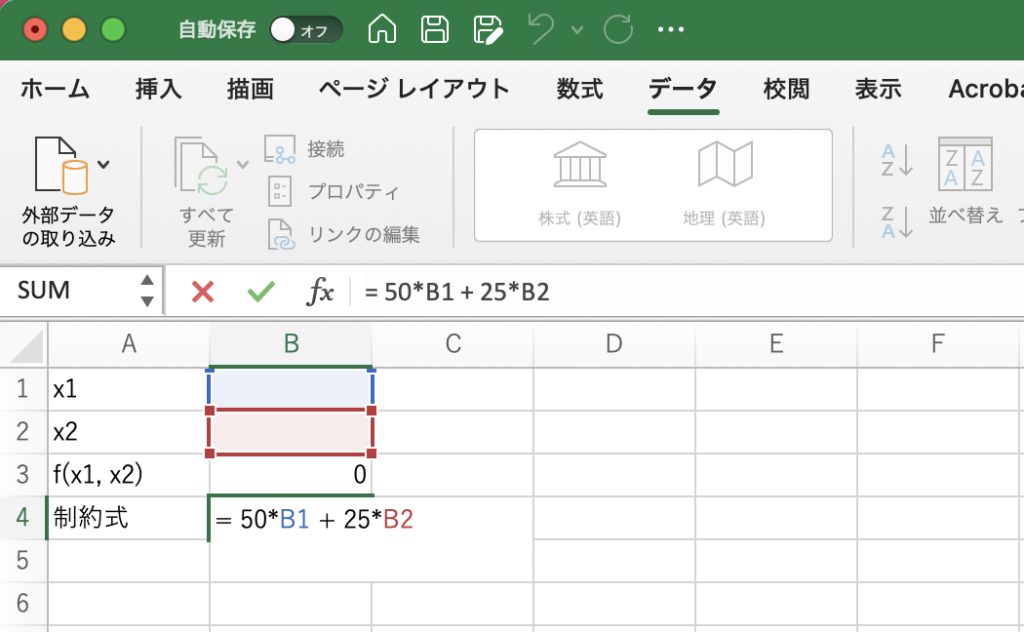
B1とB2に何も入力していないときは、両方とも0と見なされています。 ![]() なので、目的関数の値は0、制約式の左辺の値も0です。ためしに
なので、目的関数の値は0、制約式の左辺の値も0です。ためしに![]() を入れてみると、目的関数の値は1になり、制約式の左辺の値は75になります。
を入れてみると、目的関数の値は1になり、制約式の左辺の値は75になります。
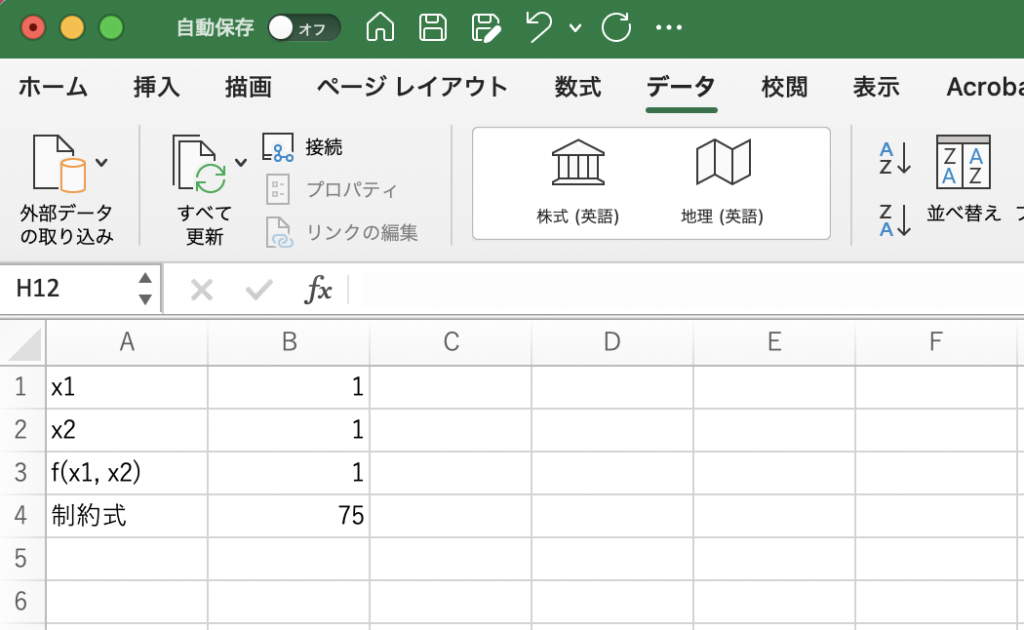
「ためしに」と言いましたが、実はソルバー が解探しをするとき、セルB1, B2にあらかじめ入っている値(これを「初期値」といいます)しだいで解が見つかったり、見つからなかったりします。![]() よりも
よりも ![]() としておいた方が、ソルバーで解が見つかりやすいので、セルB1とセルB2は1としておきましょう。ここまで準備ができたら、次にソルバー・ウィンドウを開きます。
としておいた方が、ソルバーで解が見つかりやすいので、セルB1とセルB2は1としておきましょう。ここまで準備ができたら、次にソルバー・ウィンドウを開きます。
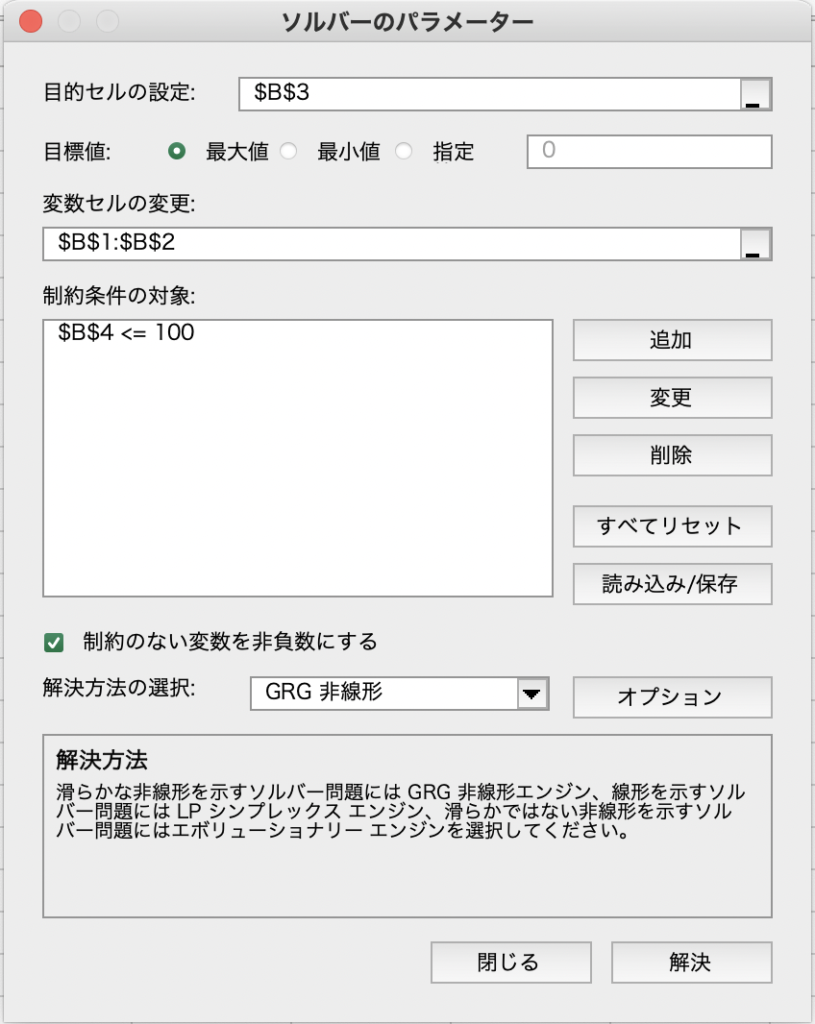
1行目の「目的セルの設定」では、目的関数のあるセルB3を選びます。
2行目は、「最大値」を選びます。
3行目の「変数セルの変更」では、セルB1,B2を選びます。
今回はさらに、制約を追加します。制約を追加するため、「追加」をクリックしてください。以下のようなウィンドウが開きます。
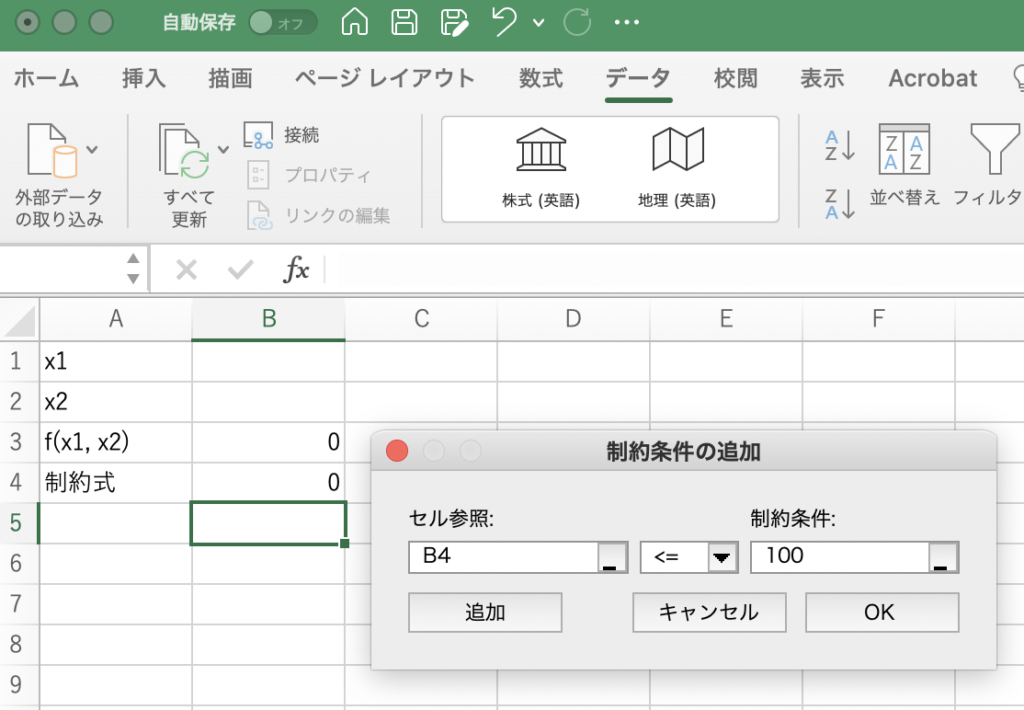
制約式の左辺にはセルB4を選び、「小なりイコール」の不等号を選び、右辺には100と入力します。OKをクリックすれば、これで制約条件が追加されます。ソルバーの解決ボタンをクリックしましょう。
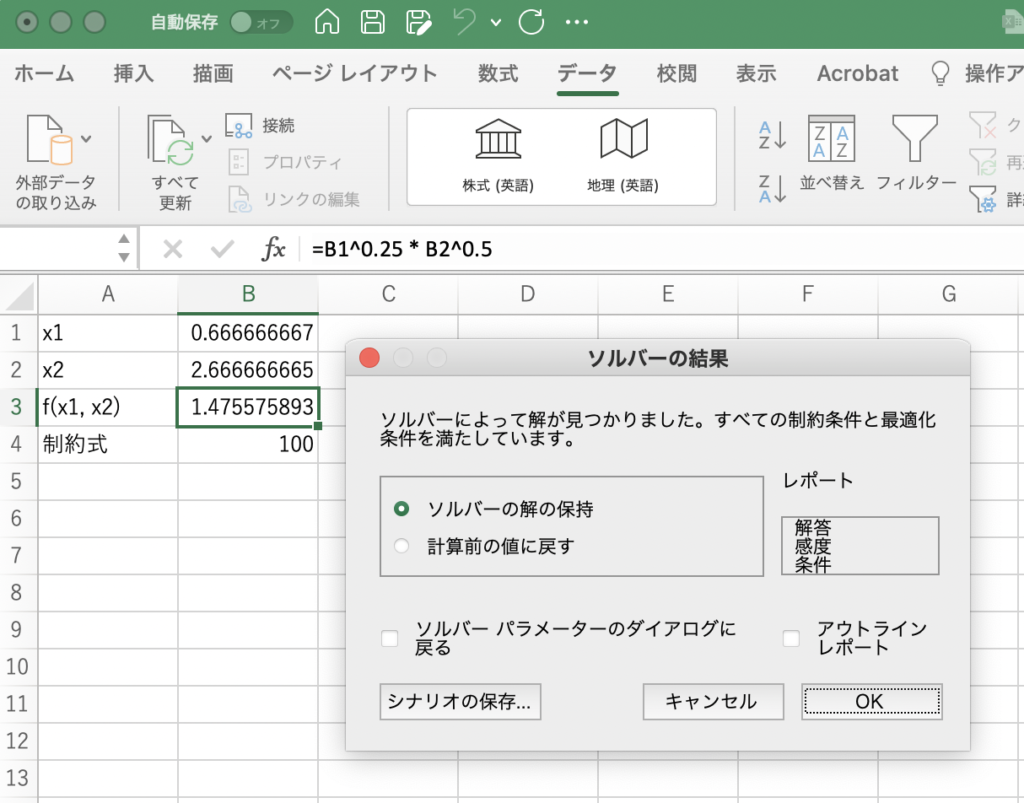
解が見つかりました。![]() ,
,![]() で、このとき制約式の左辺はちょうど100となり、不等式は等号成立しています。目的関数の値は1.4755で、これが最大値です。一連の流れは以下の動画でも確認できます。ちなみに、この例では制約式は1つでしたが、複数の制約を課すこともできます。
で、このとき制約式の左辺はちょうど100となり、不等式は等号成立しています。目的関数の値は1.4755で、これが最大値です。一連の流れは以下の動画でも確認できます。ちなみに、この例では制約式は1つでしたが、複数の制約を課すこともできます。
ソルバーが解を見つける能力は、エクセル, R, Matlabなど、ソフトウェアごとに違います。1つのソフトで複数種類のソルバーが使える場合は、ソルバーごとにも変わってきます。さらに、同じソルバーでも、初期値(出発地点)によって、解が見つけられたり、見つけられなかったりします。さきほどの例で言えば、B1=B2=0 でソルバーを使うと解が見つからないのですが、B1=B2=1 としてソルバーを使うと解が見つかるのです。解の近くから探し始めた方が見つかりやすく、遠くから探し始めると、見つかる前に時間切れになったりします。人間がしらみつぶしに物探しをする場合と似ていますね。
エクセルのソルバーは、経済学で簡単な最適化問題を解きたい時に使えるツールです。ぜひ自分でも使ってみてください。
