再帰性（５） | 午後はカフェで経済学

ジョブの現在価値

前回の練習も兼ねて、似たような例を考えてみましょう。今回は企業のジョブ（すなわち職・ポスト）を想像してください。このジョブは、各時点において「埋まっていない (“vacant”) 」か、「埋まっている (“filled”)」かの２つの状態がありえるとします。埋まっていないときは労働者を求人中、埋まっているときは誰かがポストに就いて生産活動をしています。前者を「状態0」、後者を「状態1」と呼ぶことにします。

各期に起こることは以下の通りです。

状態0のジョブは、求人・採用活動のためのコスト 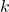$k$ がかかる。
状態1のジョブは、 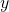$y$ 円を売上げ、労働者に 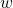$w$ 円の賃金を支払った残りの $y-w$ 円が利益になる。
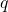状態0のジョブは、確率 $1-q$ で状態0のままであり、確率 $q$ で（適切な労働者を見つけて）状態1となる。
状態1のジョブは、確率 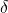$\delta$ で（労働者と別れて）状態0となるが、確率 $1-\delta$ で状態1を維持する。

例えばジョブの状態が $0\rightarrow 0 \rightarrow 0 \rightarrow 1 \rightarrow 1$ …
と変遷していったとすれば、このジョブの損益は
$(-k) \rightarrow (-k) \rightarrow (-k) \rightarrow (y-w) \rightarrow (y-w)$ …
です。採用コストは支出なのでマイナスが付いていることに気をつけてください。

割引率を $r$ として、「このジョブが将来にわたって得る利益（コストを差し引いたもの）の現在価値」を、再帰性を利用して求めます。前回の労働者の話と同様、現在価値はジョブの現在の状態が0か1かによって変わります。それぞれ $V_0$ ， $V_1$ とおきましょう。すると、前回と似たような連立方程式が成立します。練習問題として考えてみてください。

$\begin{eqnarray*}V_0 &=& -k + \frac{1}{1+r}[(1-q) V_0 + qV_1]\\V_1 &=&y-w + \frac{1}{1+r}[\delta V_0 + (1-\delta)V_1]\end{eqnarray*}$

１つめの式は、現時点で状態0のジョブの現在価値です。現在求人中なので、ただちに求人コスト $k$ がかかります。それが右辺第１項です。来期における価値は、労働者が見つからなければ $V_0$ ，労働者が見つかれば $V_1$ であり、それぞれ確率 $1-q$ と $q$ で起こるので、来期の価値は期待値では $(1-q) V_0 + qV_1$ です。１期先のことなので、それを $1/(1+r)$ で割り引いたものが右辺第２項です。

２つめの式は、現時点で状態1のジョブの現在価値です。今期 $y-w$ の利益が出、来期は確率 $\delta$ で状態0になるか，確率 $1-\delta$ で状態1のままなので、期待値では $\delta V_0 + (1-\delta)V_1$ です。 $1/(1+r)$ で割り引いて足します。

ここでも、求めるべきは $V_0$ ， $V_1$ です。そのほかの変数 ( $q$ , $\delta$ , $y$ , $w$ , $k$ ) の値が与えられれば、２変数・２式の線形連立方程式なので、 $V_0$ ， $V_1$ について解くことができます。具体的な数値例は省略します。

これで再帰性を利用して現在価値を求めるシリーズは終わりです。今後も折りに触れて、経済学における再帰性の応用例を紹介していきたいと思います。

>> 労働市場論（サーチモデル）（１）イントロ１