労働者の生涯所得1
今回は、再帰性の応用例を労働市場論の分野から紹介します。今回の例では、前々回の「割引き計算」と前回の「期待値の計算」の両方が出てきます。
永久に働き続ける労働者を想像してください。この労働者は、各時点において失業しているか、就業しているかのどちらかだとします。失業中であることを「状態0」、就業中であることを「状態1」と呼ぶことにしましょう。以下に説明する通り、労働者は、毎期状態に応じて受け取るものを受け取り、それから場合によっては状態をスイッチして次の期に進みます。
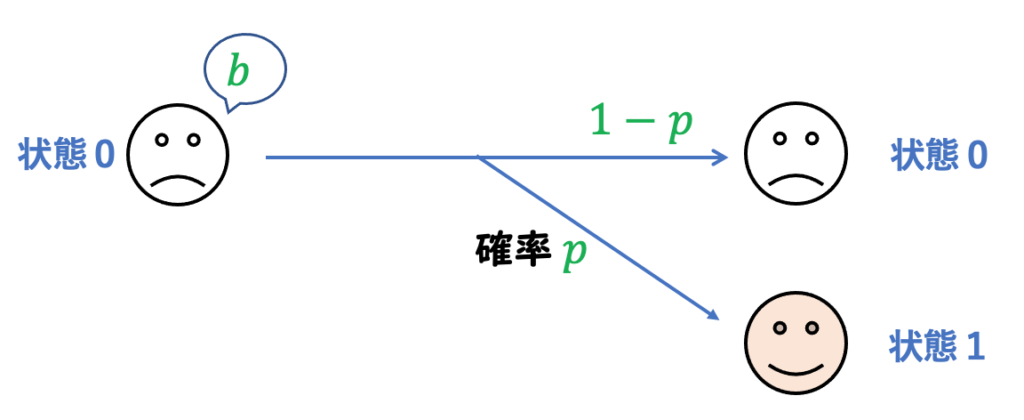
状態0のときは ![]() 円の失業保険を受け取り、その後、確率
円の失業保険を受け取り、その後、確率 ![]() で(仕事を見つけて)状態1となります。確率
で(仕事を見つけて)状態1となります。確率 ![]() で状態0のままです。
で状態0のままです。
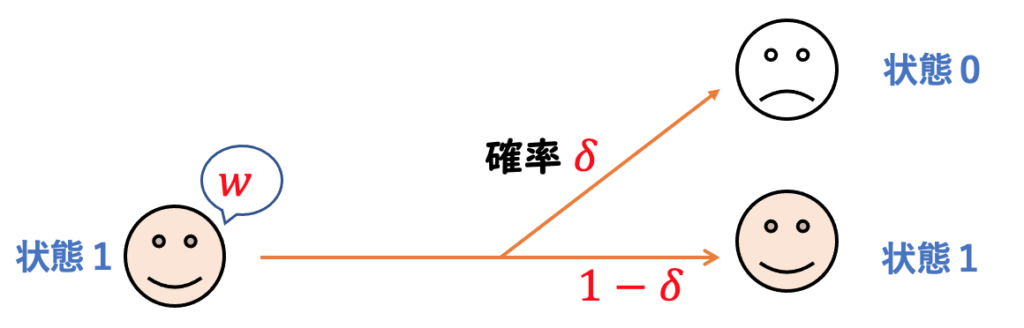
状態1のときは ![]() 円の賃金を得、その後、確率
円の賃金を得、その後、確率 ![]() で(仕事を失って)状態0となるか、確率
で(仕事を失って)状態0となるか、確率 ![]() で状態1を維持します。
で状態1を維持します。
これが毎期繰り返されます。例えば労働者の状態が![]() …
…
と変遷していったならば、この労働者が得るのは![]() …
…
です。
この労働者の生涯所得 (permanent income)、すなわち「将来にわたって得る全収入の割引現在価値」を求めましょう。割引率を ![]() として、1期後の収入なら
として、1期後の収入なら![]() ,2期後の収入ならば
,2期後の収入ならば ![]() で割り引くという点は以前と同じです。ただし、今回の割引現在価値では、将来の収入は未確定なので、収入の期待値を計算してから割引く必要があります。それを以下の図で説明しましょう。
で割り引くという点は以前と同じです。ただし、今回の割引現在価値では、将来の収入は未確定なので、収入の期待値を計算してから割引く必要があります。それを以下の図で説明しましょう。

労働者が現時点で状態0だとすると、図の一番左上にいます。すると、まず今期 ![]() 円を得ます。来期は確率
円を得ます。来期は確率 ![]() で
で ![]() 円、確率
円、確率 ![]() で
で ![]() 円なので、期待値では
円なので、期待値では ![]() 円です。
円です。![]() で割引けば来期の収入の現在価値は
で割引けば来期の収入の現在価値は![]() 円
円
です。その次の期は確率 ![]() で
で ![]() 円、確率
円、確率 ![]() で
で ![]() 円、 確率
円、 確率 ![]() で
で ![]() 円、確率
円、確率 ![]() で
で ![]() 円です。この期待値を計算して現在に割り引くと
円です。この期待値を計算して現在に割り引くと![]() 円
円
となります。この調子で、将来の各期の収入の期待値を現在に割り引いたものを無限に足し合わせたものが、現在状態0にある労働者の生涯所得です。すなわち、状態0の労働者の生涯所得を ![]() とおけば
とおけば
![Rendered by QuickLaTeX.com \begin{eqnarray*}W_0 &=& b + \frac{1}{1+r}[(1-p)b + pw]\\&+& \frac{1}{(1+r)^2} \left\{[(1-p)(1-p)+p\delta]b + [(1-p)p+p(1-\delta)] w\right\}\\&+& \frac{1}{(1+r)^3}\cdots\end{eqnarray*}](https://blog-study-economics.com/wp-content/ql-cache/quicklatex.com-dfefe9184b87149665fd9bcb5d742afa_l3.png)
このように生涯所得を正面から計算しようとすると、計算はかなり複雑です。次回は、再帰性を利用してもっと簡単に計算する方法を説明します。
>>再帰性(4)労働者の生涯所得2
