労働者の生涯所得2
前回の続きです。前回は、状態0(失業中)の労働者の生涯所得を、再帰性を用いないで求める場合を説明しました。今回は再帰性を利用します。
生涯所得は、今現在の状態が0か1かで変わってきます。現在状態0の労働者の生涯所得を ![]() とおきましょう。
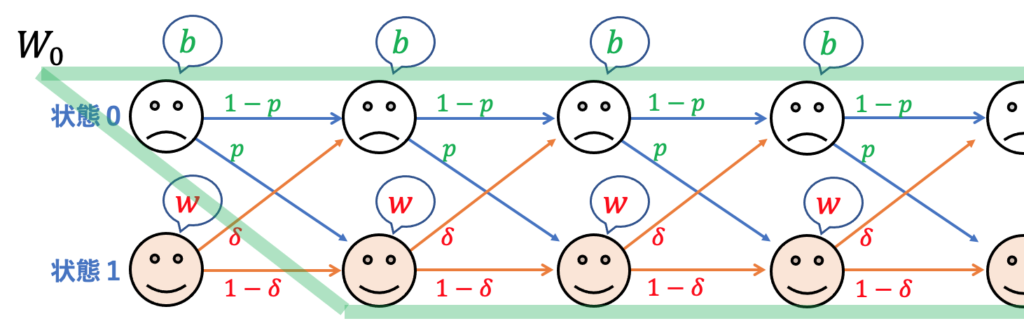
とおきましょう。![]() は、下図の緑線で囲まれた部分に含まれる全てのペイオフを算入した割引現在価値です。
は、下図の緑線で囲まれた部分に含まれる全てのペイオフを算入した割引現在価値です。
一方、現在状態1の労働者の生涯所得を ![]() とおきましょう。
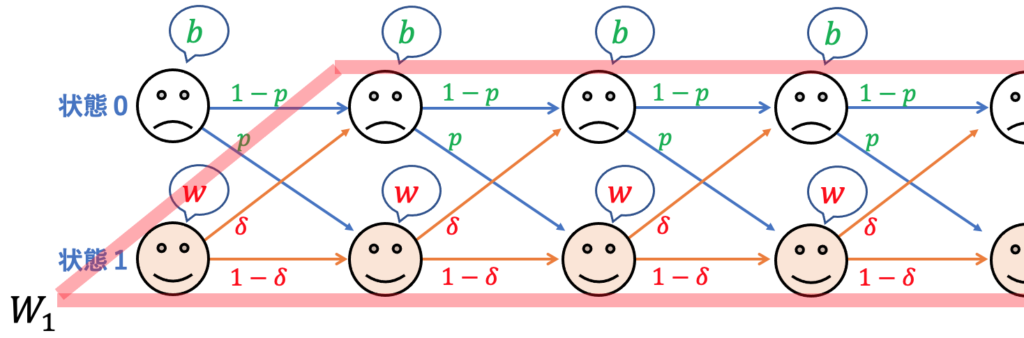
とおきましょう。![]() は、下図の赤線で囲まれた部分の全てのペイオフを算入したものです。
は、下図の赤線で囲まれた部分の全てのペイオフを算入したものです。
![]() と
と ![]() の中に、再び
の中に、再び ![]() と
と ![]() が現れることに気づくでしょうか。
が現れることに気づくでしょうか。
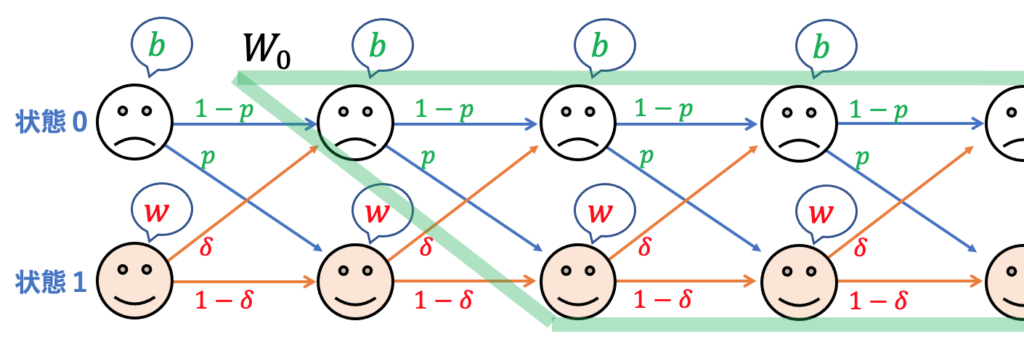
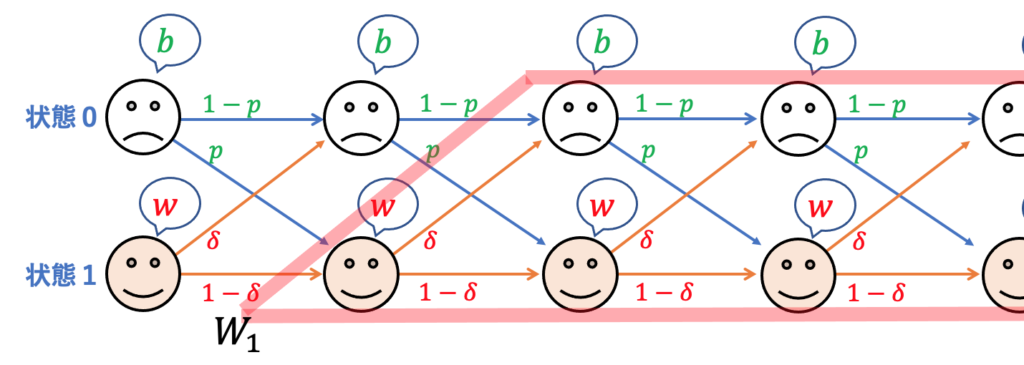
再帰性に着目すれば、![]() と
と ![]() は単純な連立方程式から求まります。まずは
は単純な連立方程式から求まります。まずは ![]() がどう表されるかを考えてみましょう。再帰性により、右辺にも
がどう表されるかを考えてみましょう。再帰性により、右辺にも ![]() ,
,![]() が登場します。
が登場します。
![]()
今現在状態0である場合、今期ただちに
次に、
![]()
現在状態1であれば、今期ただちに
![Rendered by QuickLaTeX.com \begin{eqnarray*}W_0 &=& 0.4 + \frac{1}{1.1}\left[0.6 W_0 + 0.4W_1\right]\\W_1 &=& 1 + \frac{1}{1.1}\left[0.1 W_0 + 0.9W_1\right]\end{eqnarray*}](https://blog-study-economics.com/wp-content/ql-cache/quicklatex.com-7d15afc8f65b1726ff7d43b65197f10e_l3.png)
すなわち
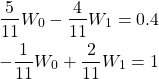
です。この連立方程式を解くと
次回は今回と似ていますが、企業側の例を考えてみたいと思います。
>> 再帰性(5)ジョブの現在価値
