目次へ

>> １，２，３，４，５

期待値の計算


今回は、確率変数の期待値の計算に再帰性を利用します。以下ようなゲームの賞金の期待値はいくらかという問題です。


図のように、1から4までの数が時計回りに並んだルーレットがあります。



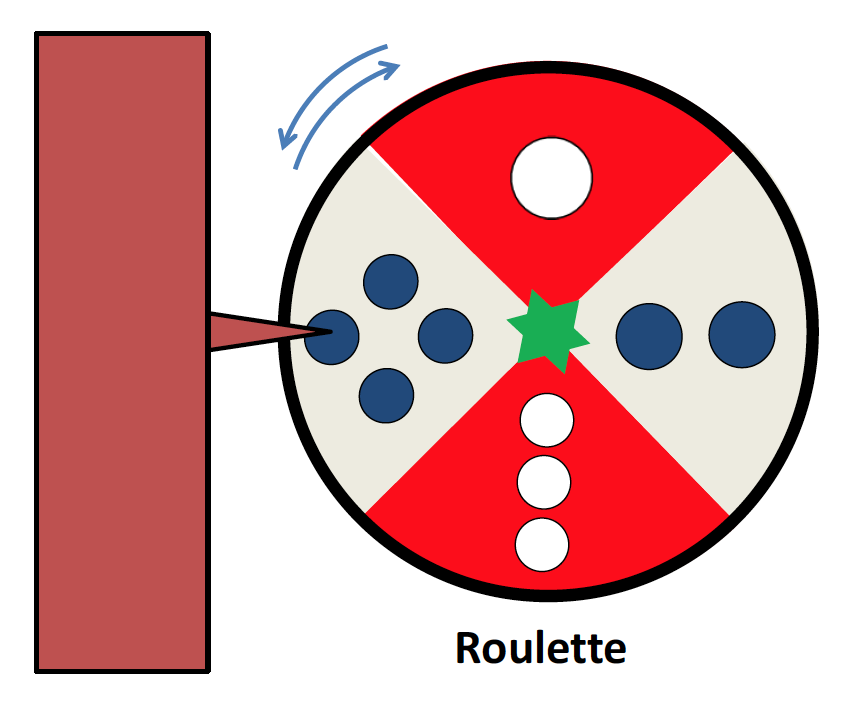
最初ルーレットは4以外の数字を指しているとしましょう。コインを投げて、表が出たら右回りに数をずらします（3は2に、2は1に、1は4になる）。裏が出たら左回りに数をずらします（1は2に、2は3に、3は4になる）。ルーレットの示す数字が4になるまでコインを投げ続け、4になった時点でゲーム終了です。ゲームの賞金は、「コインを投げた回数 \times １万円」です。最初にルーレットが1を指している状態でスタートすると、賞金の期待値はいくらでしょうか。2を指している状態でスタートした場合はどうでしょうか。


この問題に正面から挑むと、たくさんの場合分けが必要です。最初に1からスタートする場合を図示すると、以下のようになるでしょう。




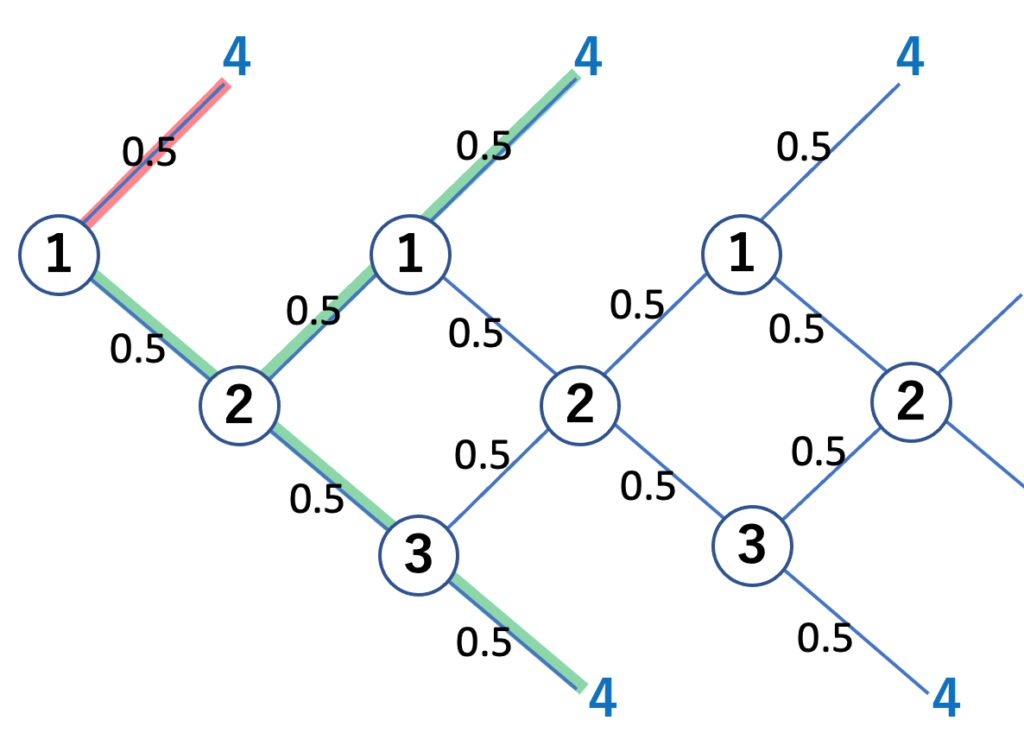
赤い線は、コインを１回投げただけでゲーム終了となるシナリオを表しています。確率は0.5です。緑の線は、コインを３回投げてゲーム終了となる２つのシナリオです。それぞれ確率(0.5)^3 です。コインを５回投げてゲーム終了となるシナリオは４通りあります。そのように全てのシナリオを網羅して計算すると、期待値は3万円、という答えが出てきます（詳細は省略）。最初に2からスタートする場合も、最初に3からスタートする場合も、同じような図を描いて考えます。


今度は「再帰性」を利用した解法です。この問題には再帰性があることに気づくでしょうか。「ルーレットが1を指しているときに、あと何回コインを投げられるか」を考えるには、次のコイン投げで表が出たらどうなるか、裏が出たらどうなるかをそれぞれ考える必要があります。表が出たら数字は4となるのでゲーム終了、裏が出たら数字は2となるので「ルーレットが2を指しているとき、あと何回コインを投げられるか」という問題を考えます。問題の中に同じ問題がある、これは再帰性です。


再帰性を利用して解くため、今、i=1，2，3の各数に関して、

\mu_i ＝「現在ルーレットが i を指しているとき、あと何回コインを投げられるかの期待値」

と定義しましょう。すると、あとで説明するように、次の式が成立します。

    \begin{eqnarray*} \mu_1 &=& 1 + \frac{0+\mu_2}{2} \\ \mu_2 &=& 1 + \frac{\mu_1+\mu_3}{2} \\ \mu_3 &=& 1 + \frac{\mu_2+0}{2} \end{eqnarray*}


\mu_1, \cdots, \mu_3 を表す式の中に再び \mu_1, \cdots, \mu_3 が出てきている所が、再帰性を利用して立てた式であることを表しています。式の意味を説明しましょう。


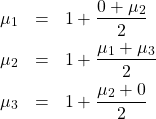
例えば最初の式は、今現在ルーレットが1を指しているときに、あと何回コインを投げることになるかの期待値を表した式です。ルーレットはまだ4を指していないので、最低でもあと１回はコインを投げられます。それが右辺の1+の意味です。コインを投げた結果、ルーレットの数字は半々の確率で2または4に変わります。2に変われば、そこからあと何回コインを投げるかの期待値は\mu_2，4に変われば 0 です。可能性は半々なので、両者の平均を取ります。それが右辺の \frac{0+\mu_2}{2} の部分に現れています。


この連立方程式を解くと、\mu_1 = 3，\mu_2=4，\mu_3 =3 という結果が出てきます。すなわち、もしルーレットが1または3を指しているならば、あと３回コインを投げられるというのが期待値であり、もしルーレットが2を指しているならば、あと「４回」というのが期待値です。最初の数字次第で、このゲームの賞金の期待値は3万円か4万円ということになります。


前回の例では「割引き計算」、今回の例では「期待値の計算」で再帰性を利用しました。次回はその両方が出てくる例として、少し経済学的な例を考えてみましょう。

>> 再帰性（３）労働者の生涯所得