確率統計の入り口（３）

<< １，２，３，４，５

「過去の平均」と「将来の平均」

「平均」という言葉には、似て非なる２種類の意味があります。ひとつは「過去のデータの平均」のことで、「前回のテストの平均点」とか、「先月の平均気温」みたいに使います。もうひとつは「これから起こることの平均」で、別名「期待値（きたいち）」と呼ばれるものです。２つの平均の違いを理解するために、次のような例を考えてみましょう。


あるテレビ番組の企画では、ゲストがサイコロを振り、出た目の数と同じだけ１万円札がもらえるとします。このサイコロは、細工のされていない、普通のサイコロです。すでに過去に１０回行われていて、その結果は1, 5, 6, 4, 4, 1, 6, 5, 6, 3 だったとしましょう。過去の平均賞金額はいくらでしょうか。10回分を合計して、10で割ればいいですね。過去の平均は万円です。


では、将来このゲームをやるあなたにとって、期待賞金額は4.5万円と言えるでしょうか。もちろん、そんなことはありません。普通のサイコロであれば、１から６までの目が等確率で出るのですから、将来の平均は万円です。6で割っているのは、それぞれの目が1/6ずつの確率で出るからです。


このように、平均には「過去の平均」と「将来の平均」の２種類あります。過去の平均は、過去のデータから求めます。100人の学生のテストの点の平均点であれば、100人の点数を合計して100で割ります。30日間の平均気温であれば、30日分の気温を合計して30で割ります。この、100人とか30日とかいった「全体数」のことを、統計学では「標本数」と言って、アルファベットのNを使って表します。全部足してNで割ったのが過去の平均です。


一方、「サイコロを振って出る目の数は、平均的には3.5になる」と言ったときの平均は「将来の平均」、つまり期待値です。未来のデータは存在しませんから、期待値を求めるときは、代わりに「確率」を使って計算します。サイコロであれば、1が出る確率は1/6，2が出る確率も1/6，… というように、それぞれの値が出る確率を使って平均を求めるのです。


もちろん、私たちは「過去の平均がこれくらいだったから、将来もそれくらいかな」と考えることもあります。しかし、そのように過去の平均を参考にして、将来の平均を推定するのは、あくまで確率についての情報が無い場合です。確率が知られているときは、将来の期待値を理論的に求めることができます。


サイコロよりももう少し複雑な例で、期待値を求める練習をしてみましょう。別の番組では、ゲストは絵のようなルーレットを回し、出た目の数と同じだけ１万円札がもらえます。賞金額は、実際にルーレットを回してみないと分かりませんから「確率変数」です。

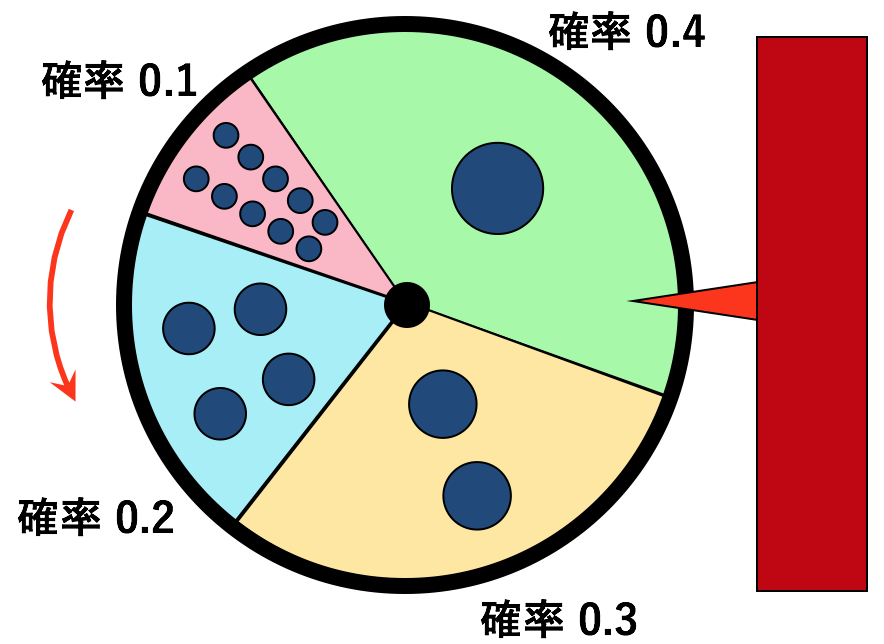
番組のスタッフはルーレットを、最高金額の10万円がなかなか当たらないように設計しました。確率分布は

10万円（確率 0.1）
4万円（確率0.2）
2万円（確率0.3）
1万円（確率0.4）

です。このゲームにこれから参加するゲストたちにとっての平均賞金額（期待値）を計算します。将来の平均ですから、過去のデータはいりません。それぞれの賞金額に、対応する確率をかけて合計して求めます。答えは万円です。確率をかけて足し合わせる作業のことを、「確率を重みにして、加重平均を求める」とも言います。


さて、過去と将来の２種類の値が存在するのは、「平均」に限りません。実は、標準偏差や相関係数もそうなのです。「過去のデータの標準偏差」に関しては以前説明しましたが、「確率変数の標準偏差」というものもあります。次回はこれについて説明します。

>> 確率統計の入り口（４）「過去のデータの標準偏差」と「確率変数の標準偏差」