e の展開公式
前回は、数学において ![]() という特別な無理数があることをお話ししました。今回から、
という特別な無理数があることをお話ししました。今回から、![]() がどんな数なのかという説明をしたいと思います。
がどんな数なのかという説明をしたいと思います。![]() のだいたいの大きさ(
のだいたいの大きさ(![]() )を思い出せたら準備オーケーです。
)を思い出せたら準備オーケーです。![]() が満たす1つめの式は
が満たす1つめの式は
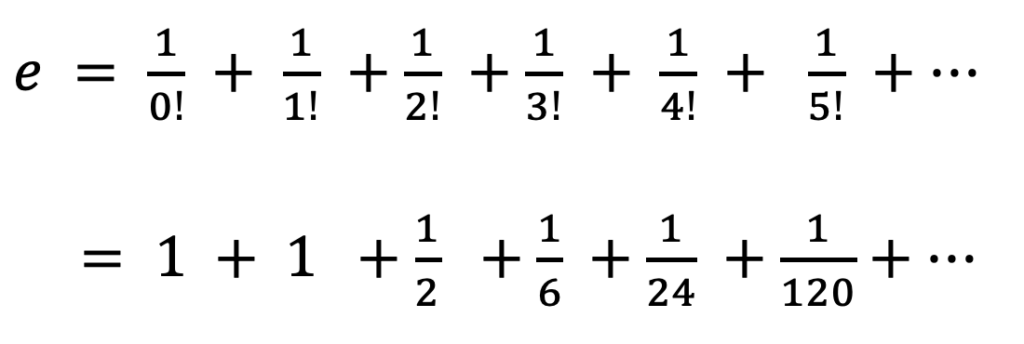
です。ここで「!」は「階乗」を表し、![]() と定義されます(
と定義されます(![]() だけは例外で、
だけは例外で、![]() という決まりです)。和のシグマ記号を使って表せば、
という決まりです)。和のシグマ記号を使って表せば、
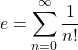
です。
ここでさらに一歩進んで、この
(1) ![]()
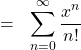
この式をグラフで表せば、以下の動画のようになります。
青い線で描かれているのが、関数 ![]() のグラフです。一方、赤い線で描かれているのが、上記の式(1)の右辺の項を1つずつ追加していったものです。すなわち
のグラフです。一方、赤い線で描かれているのが、上記の式(1)の右辺の項を1つずつ追加していったものです。すなわち
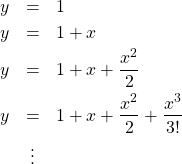
1次関数、2次関数、3次関数・・・というように次数を上げていくにしたがって、
次回は
>> オイラー数「e」(3)連続複利
