<< (1)
イールド・カーブの変化
前回は1年物から5年物までの5種類の債券があるという例を用いて「金利の期間構造」を勉強しました。それぞれの債券価格から金利を計算し、「何年物は年率何%」というふうに一覧にしたものが「金利の期間構造」で、グラフにしたら「イールド・カーブ」でしたね。前回の例で描いたイールド・カーブは、緩やかな右上がりになっていました。
今日はこのイールド・カーブの「変化」についての勉強です。債券価格が変化すると、そこから計算されるイールド・カーブも変化します。とは言っても、新しいことは何もありません。変化後の価格でもう一度イールド・カーブを描き、最初のカーブと見比べるだけです。
引き続き5種類の債券が取引されているという設定です。もともとの価格は前回と同じ、1年物から5年物まで順番に98, 96, 93, 90, 86ドルです。これが99, 96, 92, 87, 80ドルへ変化したというシナリオを考えてみましょう。1年物は価格が上がり、3年物から5年物は価格が下落した、というシナリオです。結果的に、1年物と5年物の価格差は大きくなっています。これを以下の図では「シナリオA」と呼びましょう。当初の価格が青で、価格変動後は赤で表わされています。
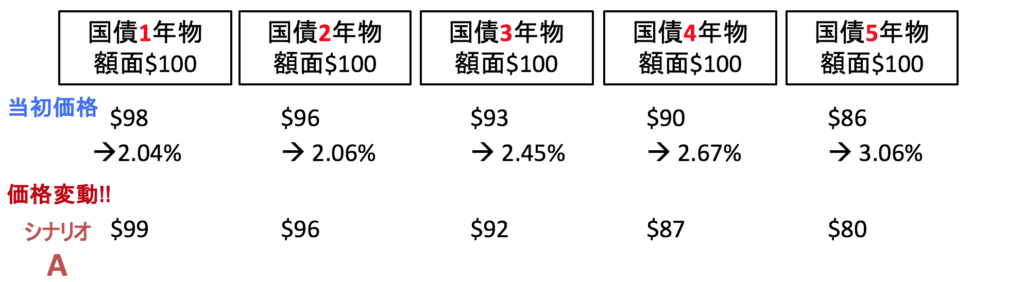
この新しい価格に関しても、金利を計算して期間構造を求めることができます。金利を求めると、1年物の金利が年率1.01%, 5年物の金利は年率4.56%です。変化前よりも1年物と5年物との金利差が大きくなっていますね。
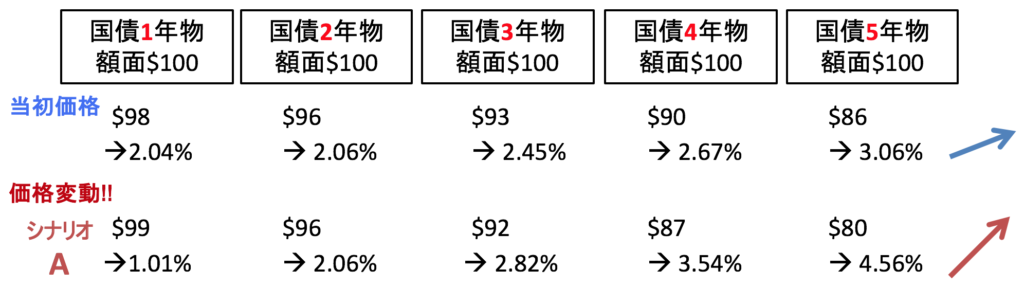
「長短金利差が大きくなった」とか、「イールド・カーブの傾きが急になった」という言い方もします。グラフにするとこんな感じです。
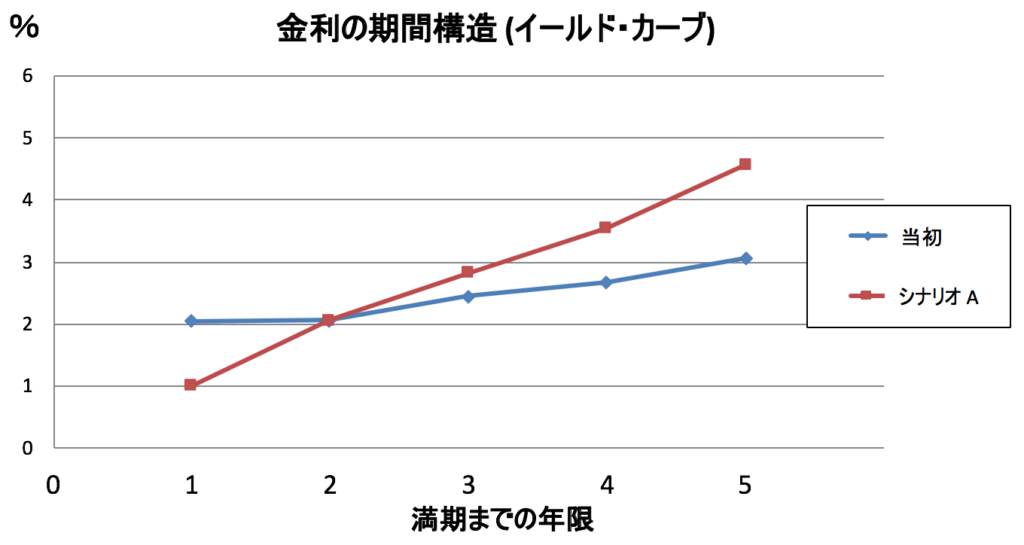
債券価格が刻々と変化するので、イールド・カーブも変化し続けます。それを毎日描いてパラパラ漫画のような動画にしている人もいます。そのような動画を見ると気がつくのは、イールド・カーブがまれに右下がりになることです。次回は右下がりのイールド・カーブについて勉強します。
>> 金利の期間構造(3)逆イールドカーブ
