最大化(2変数・制約なし)
前回は1変数関数の最適化をしました。今回は2変数関数の最適化です。例として、![]() を最大化しましょう。問題を正式に書き表すと
を最大化しましょう。問題を正式に書き表すと
![]()
です。
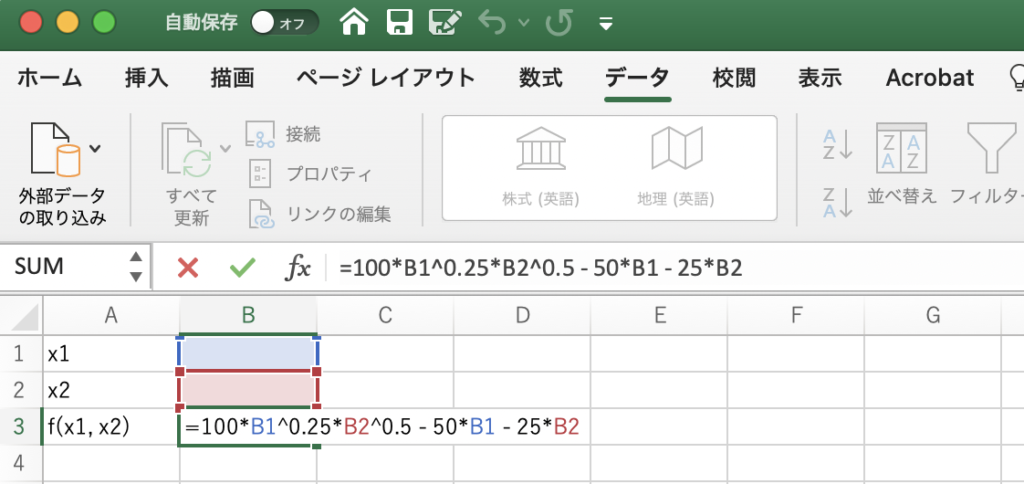
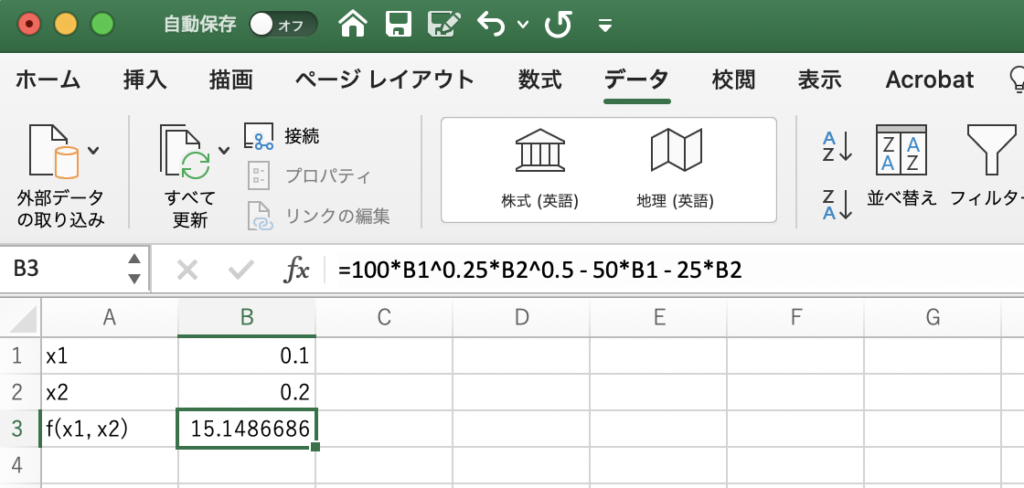
試しに ![]() ,
,![]() としてみましょう。このときの関数の値が表示されます。
としてみましょう。このときの関数の値が表示されます。
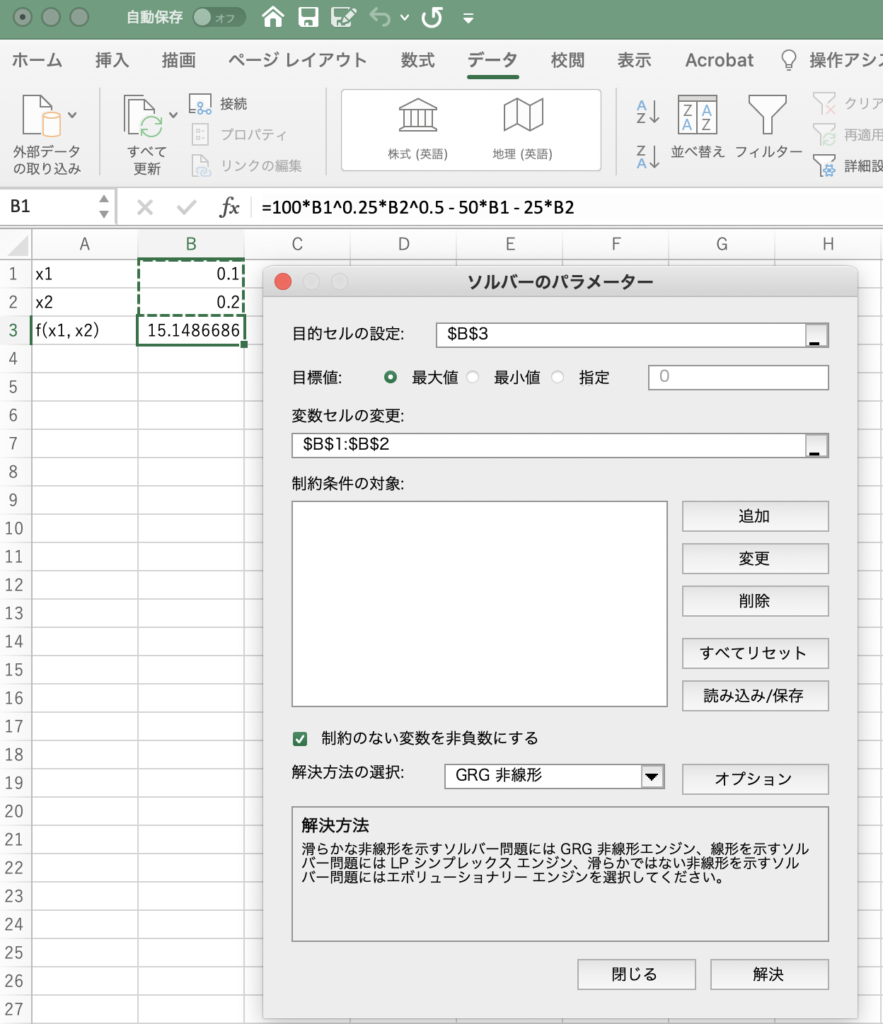
ソルバーを立ち上げ、目的関数にはセルB3、変数にはセルB1, B2を指定します。エクセルが自動で$マークを挿入することがありますが、結果に影響はありません。今回は「最大化」を選択してください。
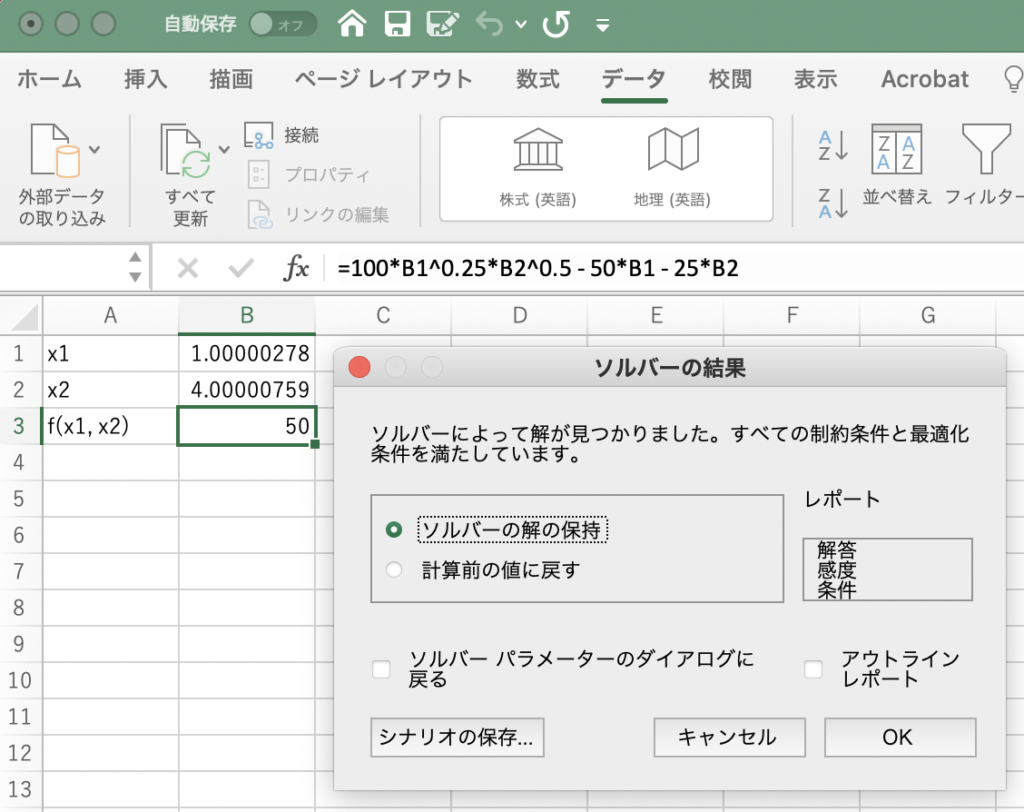
「解決」をクリックすると、ソルバー が問題を解き始め、5〜6秒後に答えが表示されます。![]() ,
,![]() のとき、最大値
のとき、最大値 ![]() になることが分かります。(数値的に解いているので、多少の誤差があります。)
になることが分かります。(数値的に解いているので、多少の誤差があります。)
これも動画で流れを確認してください。
ここまで、制約条件が無い最適化を考えてきました。次回は、制約条件つきの最大化問題に取り組みます。
>> エクセル・ソルバー(3)最大化(2変数・制約あり)
