最小化(1変数・制約なし)
数学で目にする、最大値や最小値を求める問題のことを「最適化 (optimization) 問題」と呼びます。利益の最大化やコストの最小化など、何かを最適にするためであることが多いからです。今回のシリーズでは、この最適化をエクセルの機能である「ソルバー (Solver)」を使って解く方法を勉強します。
ソルバーは、エクセルに入っている機能なので、何かを新たにダウンロードする必要はありませんが、初めて使うときには「アドインの追加」という作業が必要です。これは、書庫の奥から本を引っ張り出してくるような作業です。ソルバーをアドインとして追加する方法は、ここでは説明しませんが、いったん追加すれば、ソルバー・アイコンが「データ」項目の一番右端に現れます。
ソルバー を使って、1変数の最小化問題(制約条件なし)を解いてみましょう。
![]() を最小化するような
を最小化するような ![]() を探します。この
を探します。この ![]() のような、最小化や最大化の対象となる関数を、「目的関数 (objective function)」と呼びます。
のような、最小化や最大化の対象となる関数を、「目的関数 (objective function)」と呼びます。
最小化問題を正式に書くときは、“minimize” の頭文字 min の次に、最小化したい目的関数を書きます。
![]()
あるいは
![]()
です。min の下に書いてある
次の画像を見てください。試しにセルC4に関数を入力してみましょう。
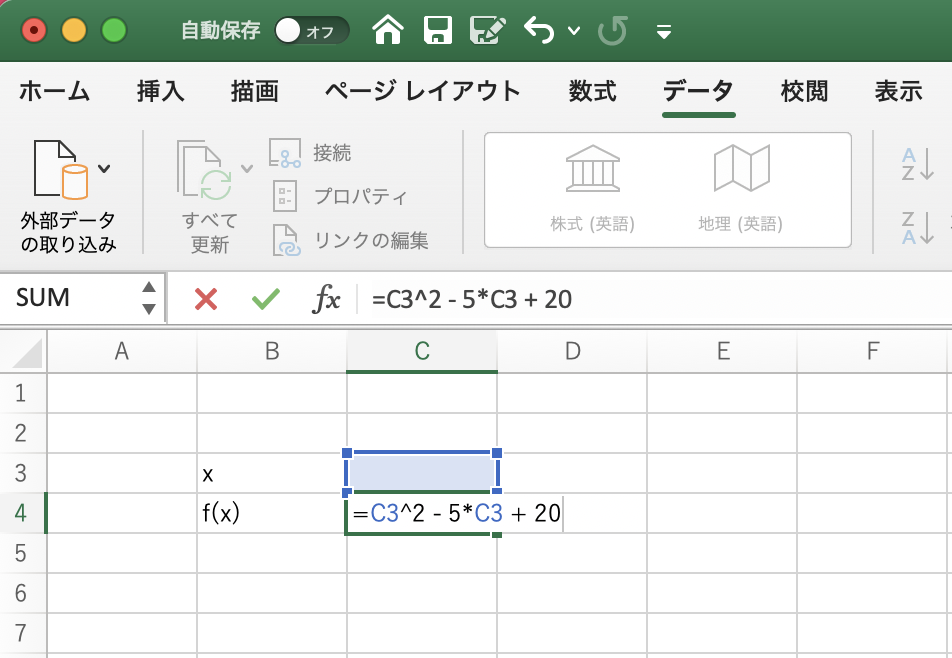
関数の入力を終えたあとは、セルC3が空白(ゼロ)のとき、セルC4の値は20となっているはずです。セルC3の値をいろいろ変えれば、C4の値も自動的に変わります。
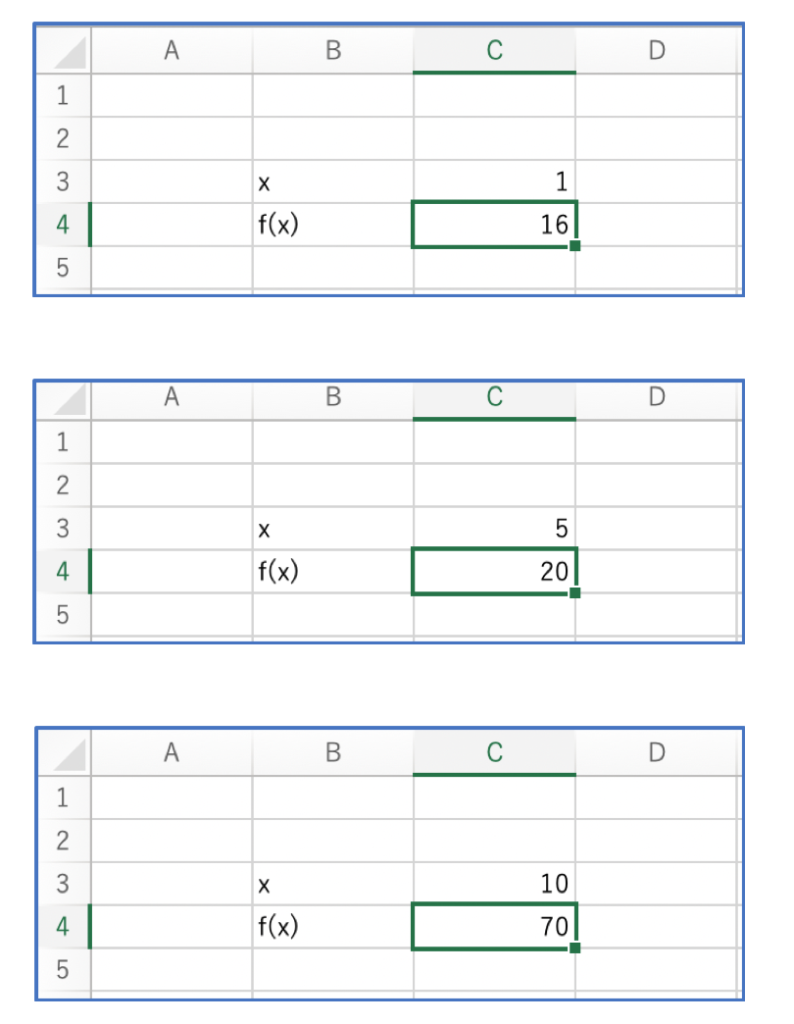
C4の値が最小になるような値を、ソルバー で見つけましょう。ソルバー ・アイコンをクリックして、ソルバー ・ウィンドウを開きます。
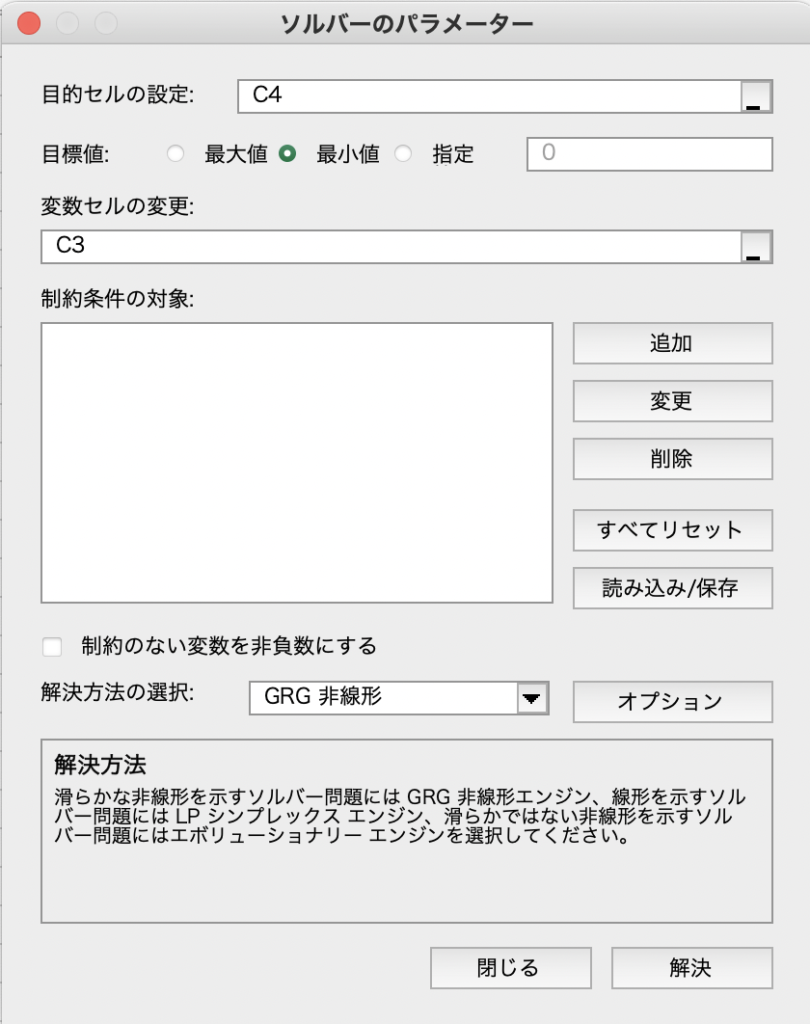
1行目の「目的セルの設定」では、目的関数が入力してあるセルC4を指定します。
2行目は「最小値」を選びます。
3行目の「変数セルの変更」はセルC3を指定します。これは、どのセルの値を変化させながら目的関数を最小化するのかということです。(エクセルが自動で $マークを挿入することがありますが、結果に影響はありません。)
今回は制約条件なしの最小化なので、その下は空白のままにしてください。最後に、「制約のない変数を非負数にする」という所のチェックを外しておきます。ここは、解 ![]() が正の値だと分かっているときのみ、チェックを入れます。今回は事前に正負がわかっていません。
が正の値だと分かっているときのみ、チェックを入れます。今回は事前に正負がわかっていません。
全て終わったら「解決」をクリックしてください。すると、ソルバー の結果が表示されます。
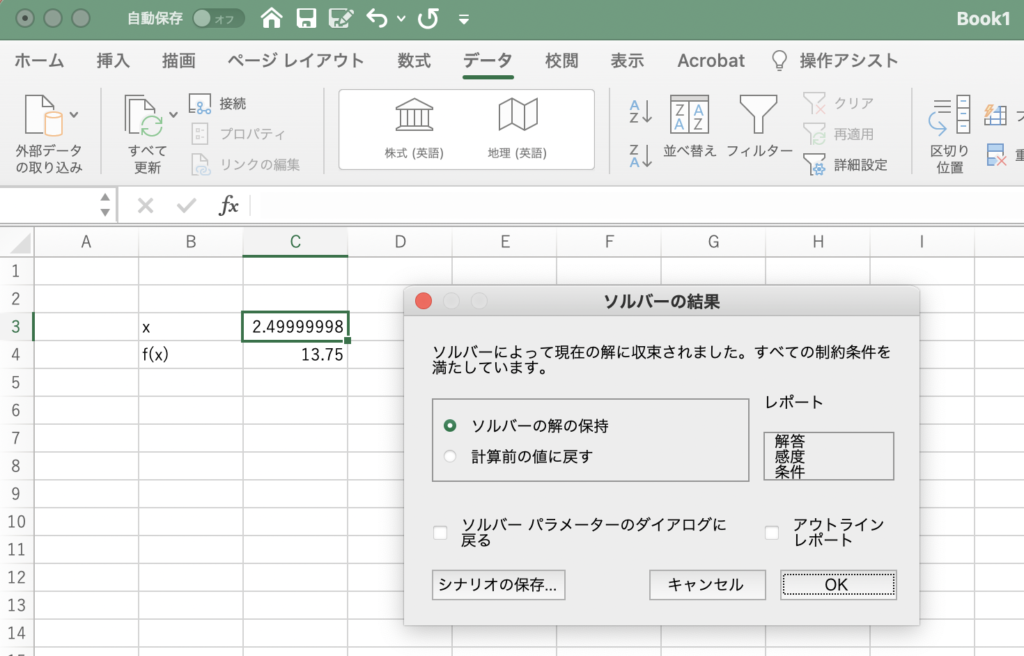
問題によってはソルバー が解を見つけられないこともあるのですが、今回は「ソルバー によって現在の解に収束されました」と出てきました。これは「解が見つかりました」という意味です。
「ソルバーの解の保持」という所にチェックがついていることを確認して、OKをクリックしてください。すると、セルC3に、ソルバー が見つけた解が表示されます。解はおよそ ![]() で、このとき目的関数の値は
で、このとき目的関数の値は ![]() です。理論的な解はぴったり2.5なのですが、コンピューターが試行錯誤しながら見つけた解なので、多少の誤差があります。
です。理論的な解はぴったり2.5なのですが、コンピューターが試行錯誤しながら見つけた解なので、多少の誤差があります。
どうでしたか。動画でも流れを確認してください。次回は2変数の関数を最大化してみましょう。
