<< １，２，３，４，５

２つの確率変数のあいだの相関係数


今回のテーマは相関係数 (Correlation coefficient) です。平均や標準偏差と同様、相関係数にも「過去のデータ」に関するものと、「確率変数」に関するものの２種類があります。前者に関しては、以前、「相関係数を知ろう」のシリーズで、生徒たちの英語の点数と数学の点数の例を使って勉強しました。今回のテーマは後者、つまり２つの確率変数のあいだの相関係数です。


とは言え、相関係数の解釈はそんなに変わりません。AとBのあいだの相関係数が大きい（１に近い）ということは、「Aが大きいときBも大きく、Aが小さいときにはBも小さい傾向がある」ということです。ちょっと変ってくるのは、計算のしかたです。そこで、確率変数どうしの相関係数の計算法を学ぶために、以下のようなルーレットの例で練習してみましょう。


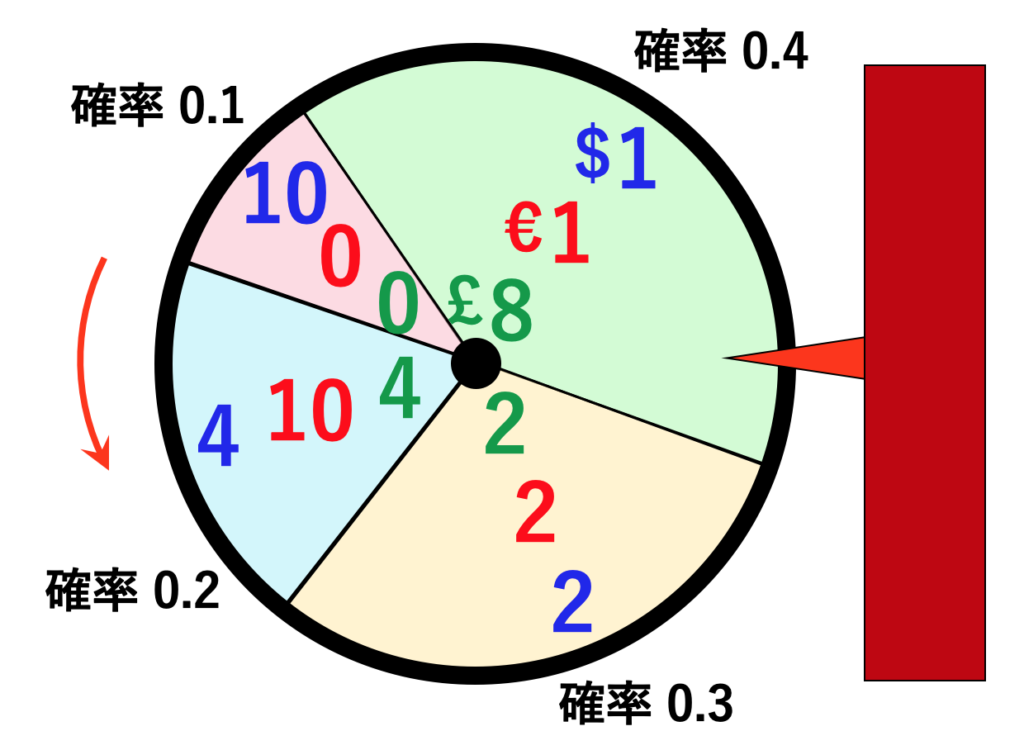
このルーレットを使ったゲームは３種類あります。「青」のゲームの賞金はドルで、$1, $2, $4, $10が、それぞれ確率0.4, 0.3, 0.2, 0.1で得られます。「緑」のゲームの賞金はポンドで、£8, £2, £4, £0が、それぞれ確率0.4, 0.3, 0.2, 0.1で得られます。「赤」のゲームの賞金はユーロです。


この例では、確率変数が３つあります。青の賞金、赤の賞金、緑の賞金です。相関係数は２つの確率変数のあいだに定義された値なので、ここでは、青と赤、赤と緑、青と緑の３通りの相関係数があります。今回の練習では、青と緑の相関を求めてみましょう。青が最も高いときに緑は最も低く、反対に緑が最高のときは青が最低なので、なんとなく負の相関が予想できますが、はたしてどうでしょうか。


相関係数を計算するための手順は４つです。
手順１：期待値と標準偏差を、青と緑それぞれについて計算する
手順２：「青の期待値からのギャップ」と「緑の期待値からのギャップ」を求める
手順３：２つのギャップの積を求め、その積の期待値を計算する
手順４：最後に、青の標準偏差と緑の標準偏差で割る


以前出てきた「過去のデータの相関係数」の計算の手順とほとんど同じです。大きな違いは、手順１と手順３で、確率を使って期待値や標準偏差を計算しているところです。


まず、手順１。青の期待値や標準偏差は、単位が「万円」から「ドル」に変わっただけで、前回と前々回にやった数値例と全く同じです。期待値は2.8ドル、標準偏差は2.64ドルとなります。緑の期待値や標準偏差も求めてみてください。期待値は4.6ポンド、標準偏差は2.97ポンドです。


手順２で求めるのは、それぞれの実現値の期待値からのギャップ（乖離）です。例えば青の賞金は確率の高い方から$1, $2, $4, $10で、期待値は$2.8なので、期待値からのギャップは順に−$1.8, −$0.8, $1.2, $7.2です。緑の賞金では、期待値からのギャップは順に£3.4, −£2.6, −£0.6, −£4.6です。


手順３では、２で求めたものを掛け合わせます。たとえば青の賞金が期待値から−$1.8ずれているときは、緑の賞金は期待値から£3.4ずれています。２つの積は−$1.8\times£3.4 = −$£6.12です。単位は消さずに、$ も£ も両方残しておきましょう。対応する確率は順番に0.4, 0.3, 0.2, 0.1なので、ギャップの積の期待値は

    \begin{eqnarray*}&&0.4(-\$1.8)\pounds3.4+0.3(-\$0.8)(-\pounds2.6)+0.2\$1.2(-\pounds0.6)+0.1\$7.2(-\pounds4.6)\\&=&-\$\pounds5.28\end{eqnarray*}


です。

手順４はこれを２つの標準偏差で割るだけですから、相関係数は

    \begin{eqnarray*}-\$\pounds5.28/(\$2.64\times \pounds2.97)=-0.673\end{eqnarray*}


となります。


相関係数の計算では、手順４で必ず単位が全てキャンセルされ、単位を持たない-1と1の間の値が出てきます。なので、もともとの値がメートルで表されているかセンチメートルで表されているかなどによって、相関係数の値が影響を受けることはありません。


ちなみにですが、手順３までやって、手順４をやる前の中途品（上の例では−$£5.28）を「共分散（Covariance）」と呼ぶので、後々のために名前を覚えてください。「共分散」を２つの標準偏差で割ると、相関係数の完成です。


ここまで、統計学では「確率分布」が存在すると信じること、そして、確率分布が分かれば期待値、標準偏差、相関係数が計算できることを説明しました。次のシリーズでは、確率変数の「期待値、標準偏差、相関係数、および分散と共分散」の５つの計算法と直観を、練習を通じて一気にマスターしてしまう作戦です。

>> 確率変数の「平・分・共・標・相」（１）舞台設定