大数の法則
コイン投げでおもて面が出る確率は確かに存在します。0.5です。神さまでなくても分かります。では、明日の東京の最高気温が30度を超える確率とか、明日の試合の第一打席でイチローがヒットを打つ確率とか、そういうものが存在するのでしょうか。「存在するさ。0.3か、0.5か、神様でもなければ正確には分からないけどね」というのが統計学の考え方です。この、「真の確率分布が存在している」という統計学の信念を支えるのが、「大数の法則」という数学の定理です。
「大数の法則」を理解するために、簡単なゲームを想像してみましょう。決められた枚数のコインを投げ、「おもて面が出たコインの割合」に100万円掛けた値を賞金としてもらえるゲームです。例えばコインの枚数が10枚であれば、あなたは10枚のコインを投げ、うち2枚がおもてだったら20万円、8枚おもてだったら80万円もらえるというルールです。
このゲームは、コインの枚数が多いほどギャンブル性が減ることが知られています。もしコインが10枚しかなかったら、2割しかおもてが出ない、なんて不運もあり得るでしょう。でもコインが100枚あったら、2割しかおもてが出ないということはありません。100枚も投げれば、おもても裏もまんべんなく出るのが普通です。
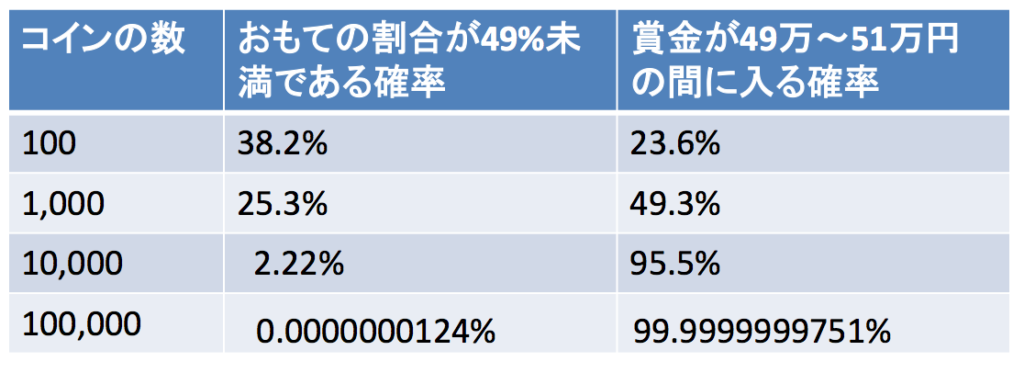
以下に、コインの枚数が100枚、1000枚、10,000枚、100,000枚の場合で2種類の確率を計算してみました。
1つは、おもてを出すコインの割合が49%に届かない確率です。100枚のコインであれば、おもての数が0〜48枚である確率。これは38.2%です。コインが100,000枚だったらどうでしょうか。おもての割合が49%に届かない、つまりおもての数が10万枚中、4万9000枚に届かない確率は0.0000000124%です。逆におもての割合が51%を超える確率も微小なので、賞金はほぼ確実に49万円と51万円の間に入ることになります。
コインを投げておもて面が出る確率が0.5であれば、コインを投げる数が増えれば増えるほど、実際におもて面が出るコインの割合も、ほとんど0.5になるのです。もしそうでなかったら大変です。女の子が生まれる確率も男の子が生まれる確率も0.5なのに、実際にはその年に生まれた100万人の赤ちゃんのうち、60万人が男の子、なんて困りますよね。数が増えれば増えるほど、実績は本当の確率に近付く、それが「大数の法則」の主張です。
大数の法則は、数学の定理であると同時に、現実の世界の法則でもあります。そのため、数学が嫌いな人であっても、現実の世界の法則としては身についています。たとえば、まだ5打席しか経験していないバッターが、そのうち2打席ヒットを打ったからといって、「このバッターの真の実力は打率4割」とは言いきれません。たまたま運が良かっただけかもしれないからです。しかし、すでに過去2年間で1000打席経験して、コンスタントに4割打っていたら、このバッターの真の実力は4割に近いと考えられませんか。もしそう考えるのなら、あなたも大数の法則を実感として知っているのです。
統計学は「確率がちゃんと存在している」と考え、「存在しているのなら、何度も試すことで推定できる」と保証してくれているのが大数の法則です。そこで私たちもここから先は、どんなものにも確率が存在している、と信じて進むことにしましょう。
さて、確率が全部ちゃんと分かっているときは、確率変数の期待値を計算することができます。次回は期待値についてお話しします。
>> 確率統計の入り口(3)「過去の平均」と、「将来の平均」

