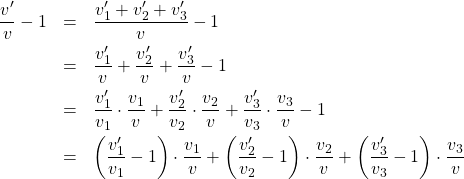資産が3種類の場合で証明します。n種類でも考え方は同じです。
A, B, Cそれぞれの株に ![]() ,
, ![]() ,
, ![]() ずつ、合計
ずつ、合計 ![]() 万円投資した結果、それぞれ価値が
万円投資した結果、それぞれ価値が ![]() ,
, ![]() ,
, ![]() になり、合計で
になり、合計で ![]() 万円になったとします。
万円になったとします。
(本文の数値例では ![]() ,
, ![]() ,
, ![]() で合計
で合計 ![]() 万円でスタートし、それが
万円でスタートし、それが ![]() ,
, ![]() ,
, ![]() で合計
で合計 ![]() 万円になりました。)
万円になりました。)
ポートフォリオの収益率は ![]() から1引いたものです。よって
から1引いたものです。よって
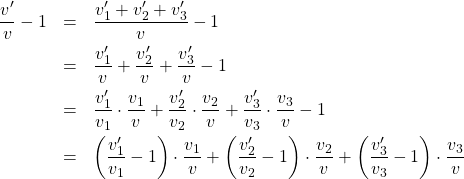
(1番目の=は
最後の式で、
<< ポートフォリオ基本用語(2)に戻る
資産が3種類の場合で証明します。n種類でも考え方は同じです。
A, B, Cそれぞれの株に ![]() ,
, ![]() ,
, ![]() ずつ、合計
ずつ、合計 ![]() 万円投資した結果、それぞれ価値が
万円投資した結果、それぞれ価値が ![]() ,
, ![]() ,
, ![]() になり、合計で
になり、合計で ![]() 万円になったとします。
万円になったとします。
(本文の数値例では ![]() ,
, ![]() ,
, ![]() で合計
で合計 ![]() 万円でスタートし、それが
万円でスタートし、それが ![]() ,
, ![]() ,
, ![]() で合計
で合計 ![]() 万円になりました。)
万円になりました。)
ポートフォリオの収益率は ![]() から1引いたものです。よって
から1引いたものです。よって