<< (2)
中間財でも最終財でもある小麦と、最終財たるパンの例
前回は、中間財でも最終財でもある「ジャガイモ」だけの世界を考えました。次の例題は、中間財でも最終財でもある「小麦」と、最終財たる「パン」の例です。前回出てきた「中間投入」と「最終需要」という言葉がまた出てくるので復習しておいてください。生産されたもののうち、原材料に消える分が「中間投入」、最終的に消費者の口に入る分が「最終需要」です。2つ合わせて「粗生産(そせいさん)」と呼ぶことにします。
例題2
小麦とパンの2種類の財しか存在しない世界を考える。今、小麦を1億円分生産するためには、0.6億円分の小麦を植えなければならない。また、パンを1億円分生産するためには0.8億円分の小麦が必要である。一方、パンが何かの原料に使われることはない。
ある国ではある年、粗生産(中間投入に使われる分と最終需要に使われる分の合計)が、小麦は200億円、パンは100億円分であった。
問1 最終需要として使われた小麦とパンの量は、それぞれいくらか。
問2 小麦産業、パン産業それぞれの貢献(付加価値)はいくらか。
解答
まず問1の解答です。次の表を埋めていきましょう。この表は、たとえば1行目を横に見ていくと、小麦生産に使われる小麦、パン生産に使われる小麦、最終需要に使われる小麦で、合計が粗の生産200億円となっています。
今、小麦の生産が200億円分ということですが、1億円分作るためには0.6億円分植えなければいけないということなので、200億円分収穫するには ![]() 億円分植えなければなりません。また、パンの生産が100億円分ということですが、これを作るには
億円分植えなければなりません。また、パンの生産が100億円分ということですが、これを作るには ![]() 億円分の小麦が必要です。したがって、小麦の生産とパンの生産に必要な分だけで、合計
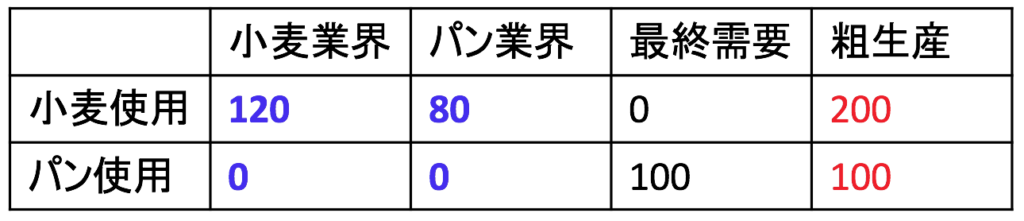
億円分の小麦が必要です。したがって、小麦の生産とパンの生産に必要な分だけで、合計 ![]() 億円分の小麦を使い果たすこととなり、原材料として使われない小麦はありません。 パンの方は中間財としては使われないので、100億円分まるまる最終消費となります。これを先ほどの表に記入すると、以下のようになります。
億円分の小麦を使い果たすこととなり、原材料として使われない小麦はありません。 パンの方は中間財としては使われないので、100億円分まるまる最終消費となります。これを先ほどの表に記入すると、以下のようになります。
文字で表した方が分かりやすいという人もいるかもしれませんね。中間投入を含めた粗の生産は、とりあえず小麦![]() 億円分, パン
億円分, パン![]() 億円分とおき、最終需要は、小麦
億円分とおき、最終需要は、小麦![]() 億円分、パンは
億円分、パンは![]() 億円分とおきます。すると以下の関係式が成り立ちます。
億円分とおきます。すると以下の関係式が成り立ちます。
![]()
ここで
さて次は問2、付加価値です。問1は財ごとに見るため、左から右に表を読みましたが、付加価値は産業ごとに見ていくので、上から下に見ていきます。小麦業界とパン業界それぞれの付加価値を見るため、上記の表の最後に2行つけ加えて以下のようにします。
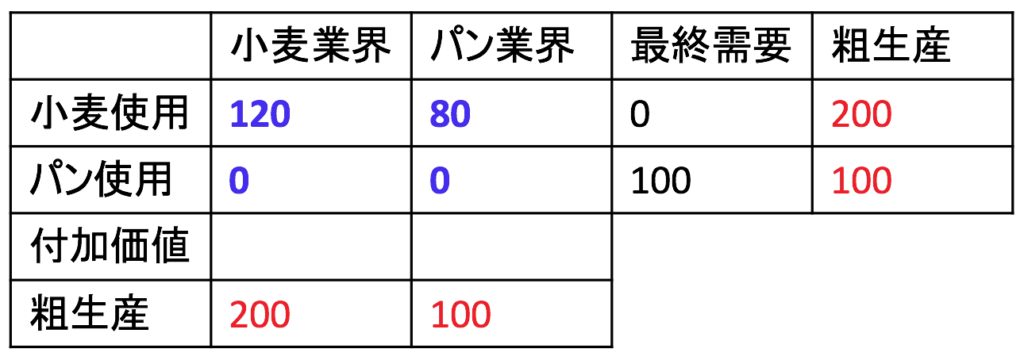
1列目は小麦業界です。中間投入の小麦120億円に、付加価値がのって、小麦の粗の生産200億円に等しくなると考えます。2列目はパン業界です。中間投入の小麦80億円に付加価値がのって、パンの粗の生産100億円に等しくなります。差額を埋めてやればそれが付加価値で、
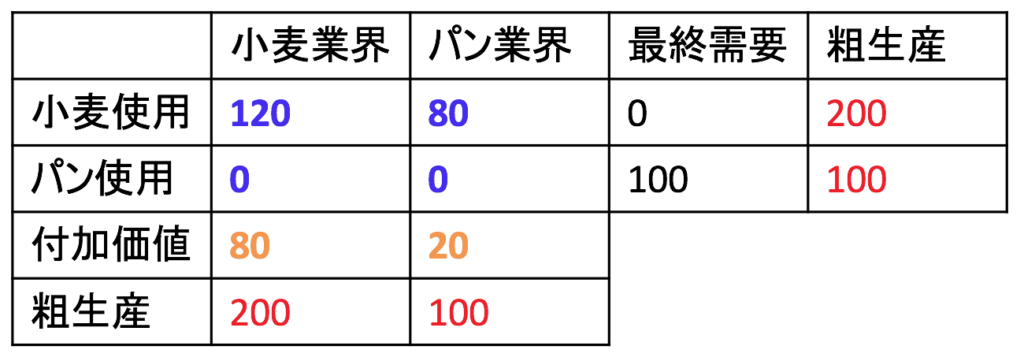
となります。小麦業界の労働者や資本家の貢献が80億円分、パン業界の労働者や資本家の貢献が20億円分です。
どうでしょうか。前回、「最終需要と付加価値は別物だ」と予告しましたが、その意味をここで確認しましょう。この例ではたまたま小麦は中間投入に使われるだけとなっています。最終需要はパンの100億円分だけです。しかし、最終的に消費者に需要されたのが100億円分のパンだけだとしても、そこには小麦業界の貢献もあるのです。小麦業界の貢献が80億円、パン業界の貢献が20億円で、合計100億です。このように、最終需要と付加価値は合計では等しくなりますが、内訳は異なります。
小麦が最終需要としても消費されるケースを練習問題としておきますので、やってみてくださいね。
練習問題:
ある国ではある年、中間投入も含めた粗の生産が、小麦は300億円、パンは100億円分であった。最終需要として使われた小麦とパンの量は、それぞれどれだけか。また、小麦産業、パン産業それぞれの貢献(付加価値)はいくらか。
次回は2つの財があって、どちらも中間投入になりうる例を勉強してみましょう。
>> GDP算出のための付加価値理論(4)中間財でもあり、最終財でもある「金属」と「機械」の例
