<< (3)
割引債は、クーポン債のバラ売り
前回は、「クーポン債は割引債のポートフォリオ(詰め合わせ)」ということを説明しました。ということは、逆にクーポン債をバラバラにして、複数の割引債としてしまうことも可能です。クーポン債をばらして作った割引債は、ストリップス債 (STRIPS)と呼ばれます。“Separate Trading of Registered Interest and Principal Securities” の頭文字を並べたものですが、英語のstripには「剥ぎ取る」という意味もあるので、バラ売りのイメージにも合っていますね。
日本の国債も含め、実際に発行される長期の債券はクーポン債が多く、割引債は元々あまりありません。しかし、クーポン債が理論的には割引債の詰め合わせに過ぎないという考え方を使えば、クーポン債の価格から割引債の理論価格を求めることができます。それはまた、クーポン債から作った割引債である、ストリップス債の価格を求めることでもあります。以下で例題を考えてみましょう。
問題
3種類のクーポン債 (A, B, C)が市場で取引されているとしましょう。それぞれの特質と価格は以下の通りです。
クーポン債Aは「満期1年・クーポンレートは1%」で額面100ドル当たり98.98ドル
クーポン債Bは「満期2年・クーポンレートは3%」で額面100ドル当たり101.82ドル
クーポン債Cは「満期3年・クーポンレートは2%」で額面100ドル当たり99.76ドル
このとき、満期が1年、2年、3年の割引債の額面1ドル当たりの理論価格はそれぞれいくらになるか、答えなさい。
解答
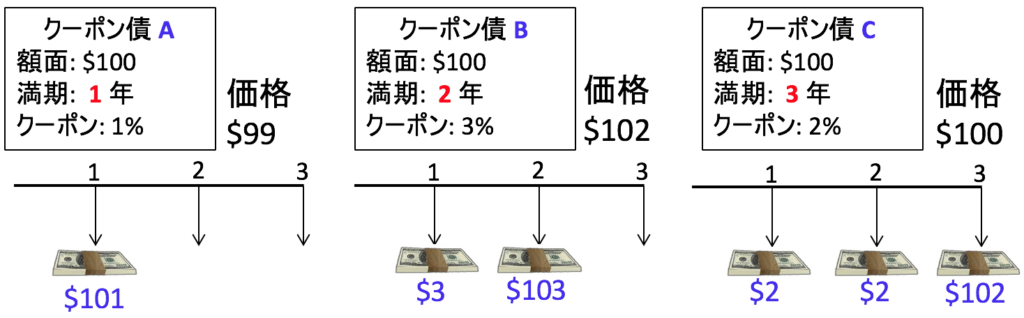
次のイラストに、それぞれのキャッシュ・フローを示しておきます。例えば債券Cならば、クーポンとして2ドルが3年間毎年支払われます。額面100ドルが支払われるのは3年目です。
今
「満期1年・額面1ドルの割引債」
「満期2年・額面1ドルの割引債」
「満期3年・額面1ドルの割引債」
をどう組み合わせればクーポン債A, B, Cになるか考えてみます。「満期が1年・額面1ドルの割引債」を101枚買えれば、1年後に101ドル受け取れます。1年後に101ドル受け取れるのは、クーポン債Aも同じです。だからクーポン債Aは、1つめの割引債101枚の詰め合わせセットです。
同じように考えると、クーポン債Bは、「満期1年・額面1ドルの割引債」を3枚と「満期2年・額面1ドルの割引債」を103枚、組み合わせた詰め合わせとみなせますね。3つのクーポン債が、それぞれ割引債のどのような組み合わせとみなせるかを図解するとこうです。

満期が1年、2年、3年の割引債の額面1ドル当たり価格をそれぞれ![]() ドル、
ドル、![]() ドル、
ドル、![]() ドルと置いて、
ドルと置いて、![]() を求めましょう。上の図より、クーポン債Aを複製する詰め合わせセットの価格は
を求めましょう。上の図より、クーポン債Aを複製する詰め合わせセットの価格は![]() ドル、クーポン債Bを複製する詰め合わせの価格は
ドル、クーポン債Bを複製する詰め合わせの価格は![]() ドル、クーポン債Cを複製する詰め合わせの価格は
ドル、クーポン債Cを複製する詰め合わせの価格は![]() です。実際のクーポン債A, B, Cの市場価格はそれぞれ98.98ドル、101.82ドル、99.76ドルと問題文で与えられていますから、「一物一価」のもとでは次の式が成立します。
です。実際のクーポン債A, B, Cの市場価格はそれぞれ98.98ドル、101.82ドル、99.76ドルと問題文で与えられていますから、「一物一価」のもとでは次の式が成立します。
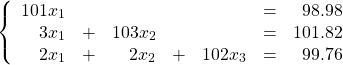
この連立方程式を解くと、![]() です。つまり、1年後に1ドルもらえる割引債の価格は0.98ドル、2年後に1ドルもらえる割引債の価格は0.96ドル、3年後に1ドルもらえる割引債の価格は0.94ドルです。
です。つまり、1年後に1ドルもらえる割引債の価格は0.98ドル、2年後に1ドルもらえる割引債の価格は0.96ドル、3年後に1ドルもらえる割引債の価格は0.94ドルです。
このように、実際に市場で価格がついて取引されているものがクーポン債であったとしても、各年限の割引債の理論価格が求まります。割引債の価格が分かれば、イールド・カーブを求めることもできますね。
クーポン債を勉強したら、最終利回りやデュレーションについても勉強できます。次は最終利回りを勉強しましょう。
>> 最終利回り(1)準備
