<< (2)
クーポン債は、割引債の詰め合わせセット
今回は、クーポン債の価格を、割引債の価格から理論的に導出する方法を学びます。割引債の価格が分かっていると、クーポン債の価格は自動的に分かってしまうというのが要点です。
ひとまずクーポン債のことは忘れて、さまざまな割引債が市場で取引されている状況を考えてください。現在の取引価格は1年物が0.98ドル、2年物が0.96ドル、3年物が0.94ドルとします。それぞれの割引債のキャッシュフロー(お金の支払額と支払いのタイミングのことです)を確認しておきましょう。次の図は額面1ドル当たりのキャッシュフローです。割引債ですから、満期に額面が支払われるだけですね。
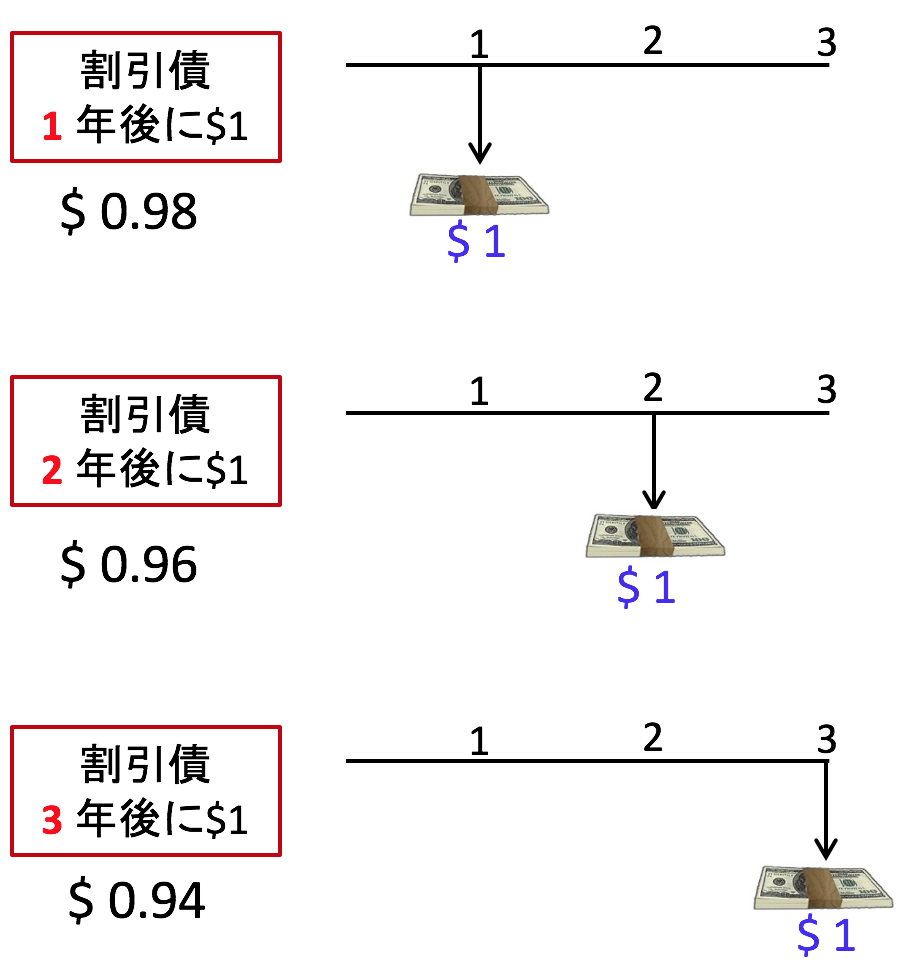
例えば、今0.98ドル払って1年物の割引債を1枚買えば、1年後に1ドルもらえます。9.8ドル払って10枚買えば、1年後に10ドルもらえます。2年後にもお金を受け取りたければ、2年物の割引債も買う必要があります。2年後に1ドル受け取るには今0.96ドル払って1枚、10ドル受け取るには9.6ドル払って10枚買う必要があります。
それでは問題です。1年後に10ドル、2年後にも10ドル、3年後には110ドル受け取りたい場合、今いくら払えばいいでしょうか。言い換えると、「1年物の割引債10枚、2年物の割引債10枚、3年物の割引債110枚」のセットの値段はいくらでしょうか。それぞれの単価と枚数を掛けて足し合わせるだけなので、難しくありません。
(1) ![]()
が正解です。
さて、今度は割引債のことをいったん忘れ、クーポン債をイメージしてください。「額面100ドル、クーポンレート10%、満期3年」のクーポン債を発行することを考えてみましょう。そのようなクーポン債の価格はいくらが妥当でしょうか。額面100ドルの10%は10ドルなので、キャッシュフローは次の図のようになります。最後の年は、クーポンの10ドルと額面100ドルの両方が支払われることに注意してください。
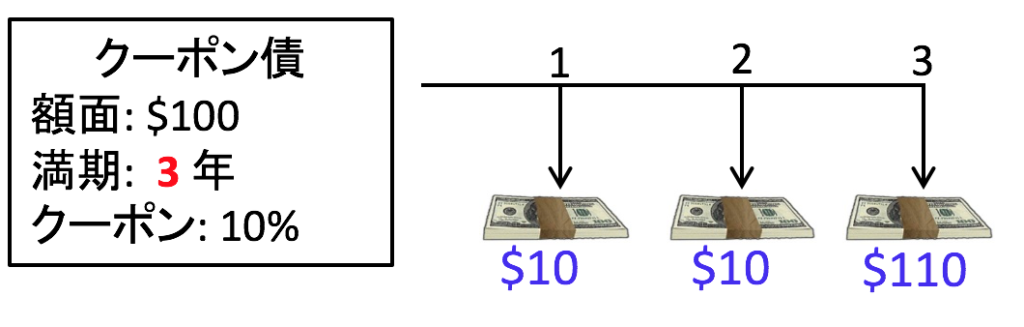
さあ、ここからがポイントです。このクーポン債は、ついさっき練習問題で価格を求めた「割引債の詰め合わせセット」と本質的に同じものです。キャッシュフローの額とタイミングが全く一緒だからです。
ファイナンスでは、ある証券のキャッシュフローを、別の証券の組み合わせで実現することを、証券の「複製」と言います。ここの例では、上の絵のクーポン債は、3種類の割引債をそれぞれ10枚、10枚、110枚組み合わせることで複製できるのです。そのような詰め合わせセットの価格は122.8ドルでした。経済学では、同じ物には同じ価格が付くという「一物一価」を仮定しますので、クーポン債の方も122.8ドルになるはずだと考えます。
理論のエッセンスは、クーポン債は複数の割引債の詰め合わせ(ポートフォリオ)であるという点に尽きます。だから、リンゴ、バナナ、みかん1個1個の価格から詰め合わせの価格が出てくるように、割引債価格からクーポン債価格が出てくるのです。
割引債とクーポン債。どちらがニワトリでどちらがタマゴか分かりませんが、次回は逆に、クーポン債の価格から割引債の価格を求めてみましょう。
>> クーポン債の理論(4)割引債は、クーポン債のバラ売
