相関係数を調べた研究例
前回学んだ相関係数の表（相関行列）が実際の研究でどのように使われるか、一例を見てみましょう。千葉 (2009) (*注1) では296名の大学生を対象にした、体力診断テストのデータを使った結果が報告されています。
以下はそこで報告されている相関行列です。「身長」や「体重」など体格を表す変数が３つ、テストの種目が６つで、合計９個の変数間の相関係数が並んでいます。
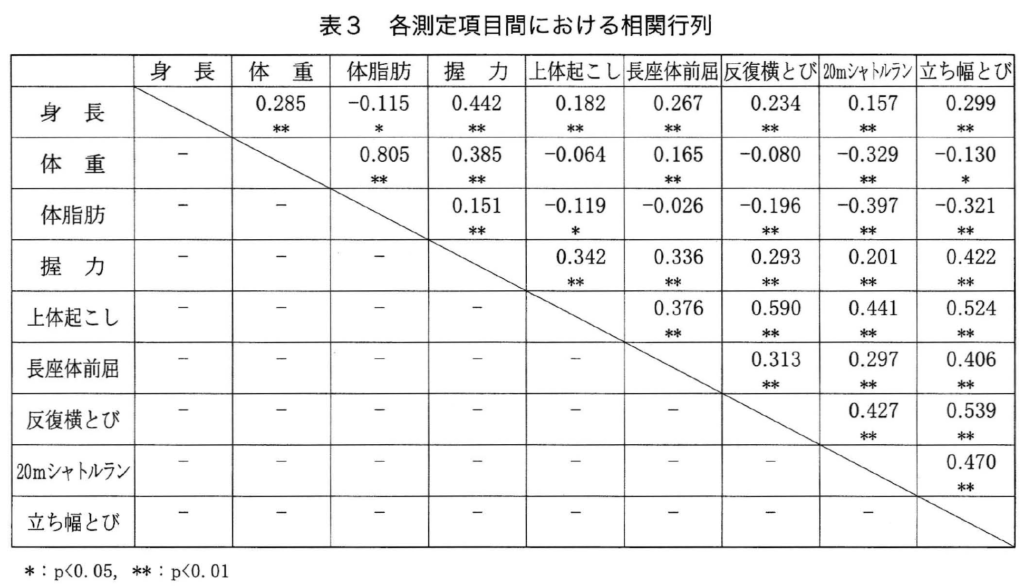
千葉さんの研究によれば、たとえば体重と体脂肪の間には0.805という高い正の相関が見られます。表の中に数字を見つけられますか？
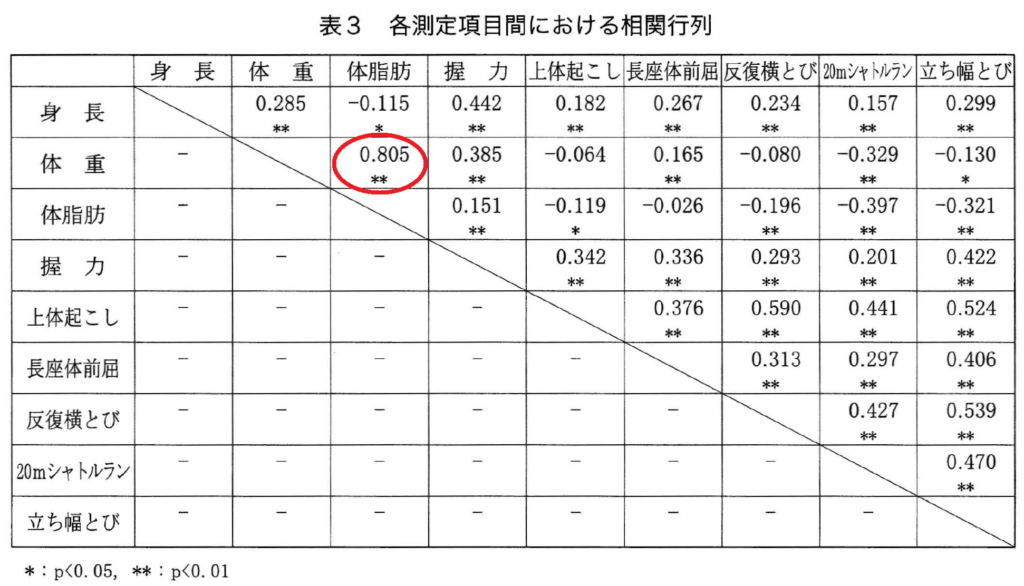
一番上の身長の行を横に見ていくと、身長が高い人は握力が強く（相関0.442）、立ち幅とびも得意である（相関0.299）ことがわかります。この辺りは私たちのイメージと一致しますね。
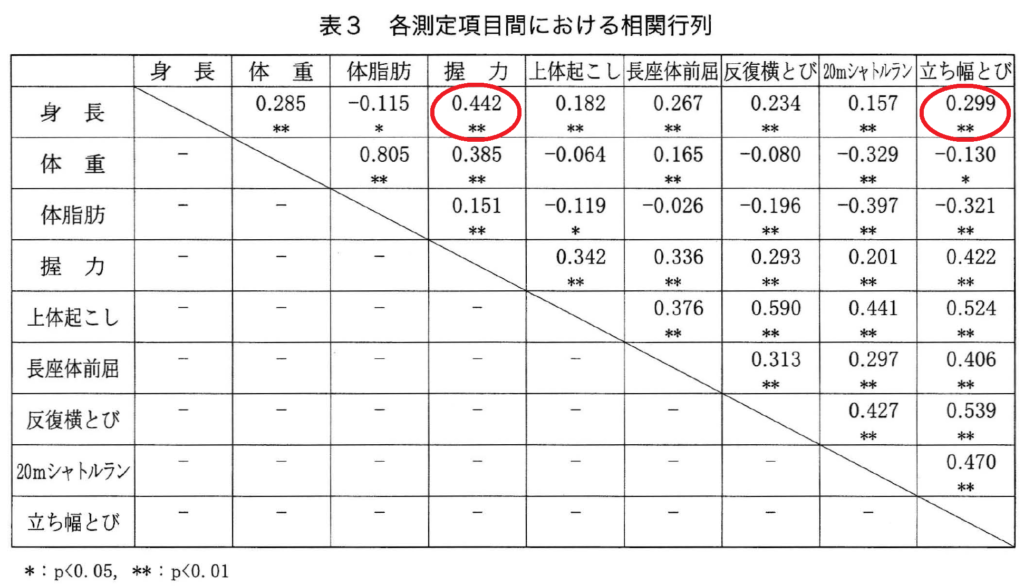
２０メートルシャトルランは、持久力を測るためのテストです。とても過酷なテストで、体重との相関が
と、負になっていることは納得できます。
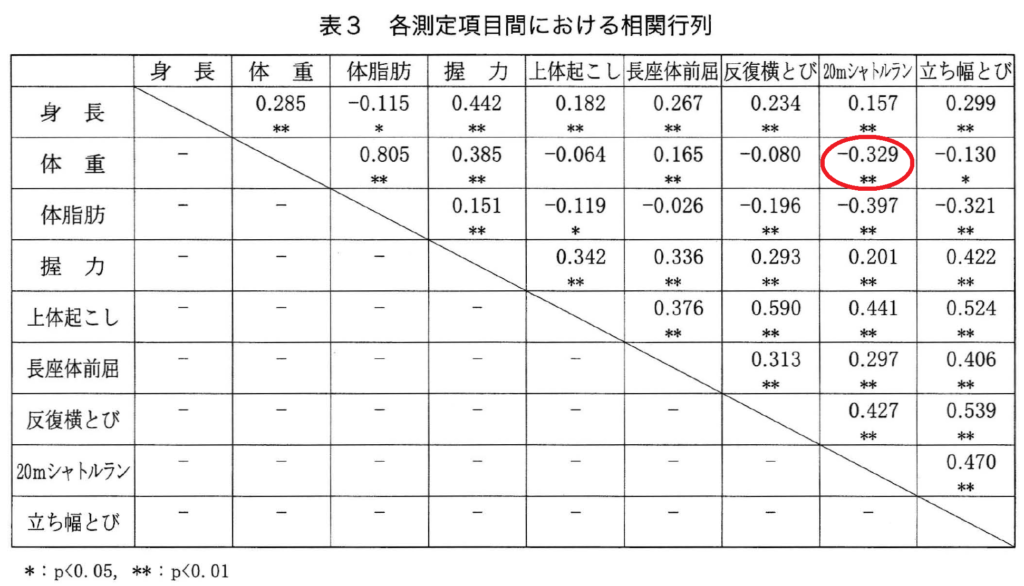
反復横とびと立ち幅とびの相関は0.539と高めです。
この理由は、「背の高い人はどちらも得意だから」かもしれませんし、「足の筋力がある人はどちらも得意だから」かもしれませんね。
面白いのは「上体起こし（腹筋）」と「反復横とび」の相関が0.590と高めなことです。
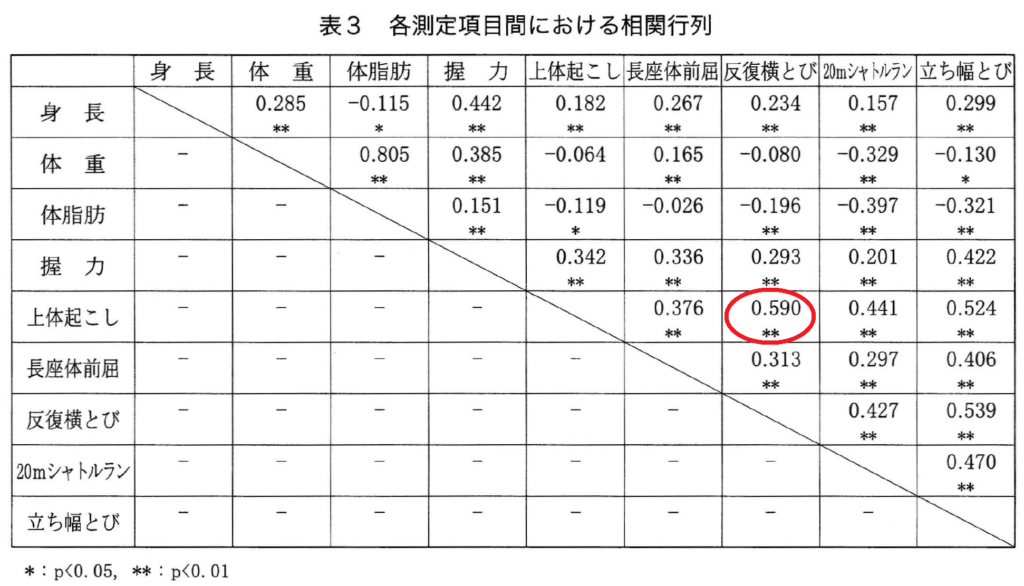
上体起こしは主に腹筋の持久力を測定するものです。千葉 (2009) の研究結果では、上体起こしは身長、体重、体脂肪といった体格との相関が低く、体格だけでは説明がつきにくい種目です。腹筋がある人は敏しょう性もあるという傾向は面白いですね。
相関係数は２つの変数の間の「連動性」「結びつき」などの強さを
から1の間の数字で表してしまおうという大胆な話です。天候と頭痛の強さ、背の高さと収入、親が子供に本を読み聞かせる時間の長さと子供の成績、なんでもいいのです。この相関係数がもっと世の中に知られれば、いろいろな面白い相関に関する研究が、もっと人々に紹介されることでしょう。
強い相関関係が見出されると、「なんでこの２つは相関しているんだろう」と理由を考えますね。そこで次回は、相関関係の理由を考えるときの注意点についてお話ししたいと思います。
>> 相関係数を知ろう（５）どっちがどっちに影響？
(注1) 千葉義信 (2009) “大学生の体格と体力の関係について” 国際経営論集 No.38, pp133-139