<< （１）
複利計算の公式
たとえば、金利５％で100万円を借りたら、返済額はいくらでしょうか。
貸借期間が１年間の場合：
万円
貸借期間が２年間の場合：
万円
と経済の授業では習いますね。でもこれは厳密に言うと、金利の複利計算を行う頻度が年１回、という前提がある場合です。
本当は複利計算の頻度によって、返済額が変わってきます。金利５％で１年間借りるのだとしても、複利計算の頻度が年に１回なのか、２回なのか、12回なのか、360回なのかによって、１年後に返す金額は変わってくるのです。
公式を書いてしまうと、以下のようになります。
金利（年率）：
複利頻度：年
回
貸借期間：
年間
とし、右辺は「金利５％・年12回複利で1.5年間」の場合の例です。
複利計算の公式
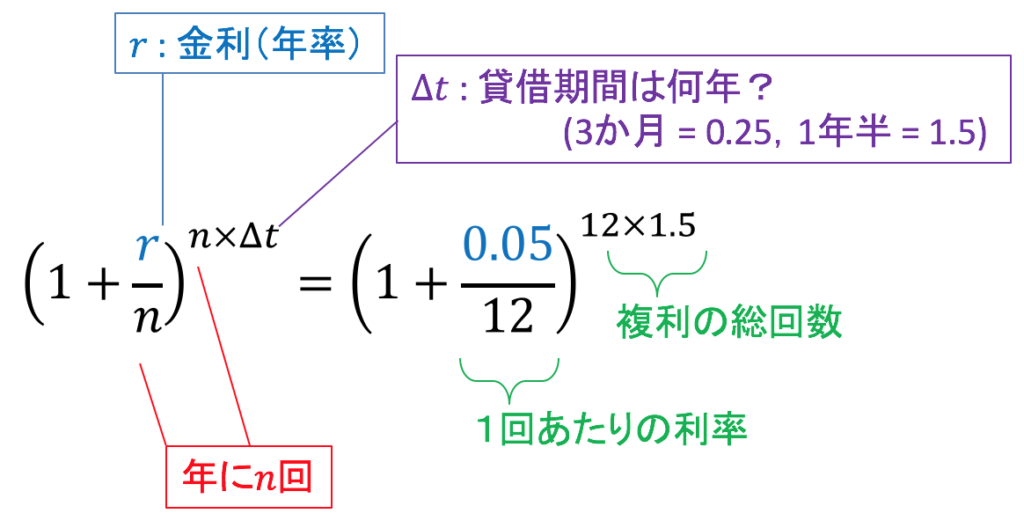
複利の頻度と貸借期間（何年間借りるのか） をかけたものが、複利の総回数です。たとえば年12回複利で１年半の契約ならば、その間に複利計算は
回起こります。一方、複利１回あたりの利率は、年率の金利を複利頻度で割ったものです。ここの例では「年５％ (=0.05)」を年12回で割って、
(=0.42％) を使います。
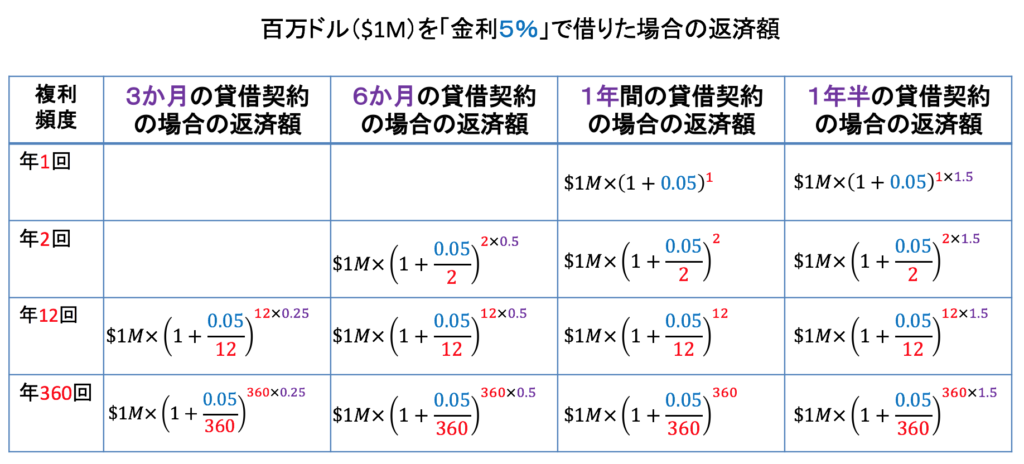
この公式で求めた数字を、借りた金額に掛けたものが、返済額の理論値となります。以下の表に、百万(1M)ドル借りた場合の返済額をまとめておきましょう。この表でも、さっきの公式と同じ色（金利は青、貸借期間はむらさき、複利の頻度は赤）が使われています。３ヶ月は0.25年、６ヶ月は0.5年と表されていることに注意してください。
さて前回、「複利計算の頻度の違いは、理論的にはそれほど大事でない」という話をしました。ただ、ファイナンス理論を勉強する人も知っておくべき、複利計算の理論的なことが２つあります。次回はそのことについて話したいと思います。
>> 金利の複利計算公式（３）複利計算の理論的なこと